Kezdőlap


Feladat:	B.4891	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Nagy Nándor , Olosz Adél
Füzet:	2018/március, 154 - 155. oldal		PDF \| MathML
Témakör(ök):	Feladat, Beírt kör, Síkgeometriai bizonyítások, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 2017/szeptember: B.4891

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Használjuk az ábra jelöléseit.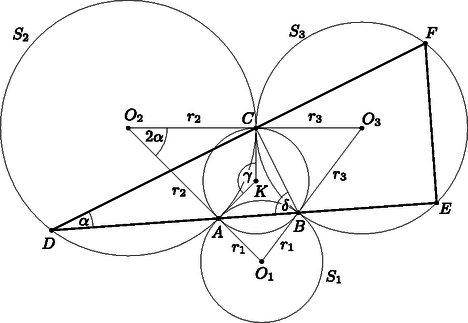

O_{1} O_{2} O_{3}

háromszög oldalait az

A

B

C

pontok úgy osztják fel, mint a háromszög beírt körének érintési pontjai, hiszen

O_{1} A = O_{1} B = r_{1}

O_{2} A = O_{2} C = r_{2}

és

O_{3} B = O_{3} C = r_{3}

. Ezért az

A B C

háromszög körülírt köre éppen az

O_{1} O_{2} O_{3}

háromszög beírt köre.
Legyen

A D C ∢ = α

. Ekkor a kerületi és középponti szögek tétele miatt az

A C

ívhez tartozó középponti szög:

{A O}_{2} C ∢ = 2 α

. Mivel

K

a beírt kör középpontja,

O_{2} A

és

O_{2} C

pedig érintők, azért

O_{2} C K ∢ = 90^{\circ}

és

O_{2} A K ∢ = 90^{\circ}

, mert az érintők merőlegesek a sugarakra. Ebből adódik, hogy az

A O_{2} C K

négyszögben, ami egy derékszögű deltoid,

C K A ∢ = γ = 180^{\circ} - 2 α

. Ez a szög középponti szög az

A B C

háromszög körülírt körében, ezért az

A C

ívhez tartozó kerületi szög:

\begin{matrix} A B C ∢ = δ = \frac{180^{\circ} - 2 α}{2} = 90^{\circ} - α . \end{matrix}

B C D

háromszögben

B C D ∢ = 180^{\circ} - α - (90^{\circ} - α) = 90^{\circ}

.
A

B C F E

húrnégyszögben

B C F ∢ = 180^{\circ} - B C D ∢ = 90^{\circ}

, ezért a vele szemben lévő

B E F ∢

90^{\circ}

, vagyis a

D E F

háromszög derékszögű. Ezt kellett bizonyítani.

Olosz Adél (Pécs, PTE Gyak. Alt. Isk., Gimn., Szakgimn. és Óvoda, 11. évf.) és
Nagy Nándor (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 10. évf.)
dolgozata alapján