Kezdőlap


Feladat:	2017. évi Kürschák matematikaverseny 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2018/február, 71 - 73. oldal		PDF \| MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd), Síkgeometriai számítások trigonometria nélkül, Geometriai valószínűség, Ceva-tétel
Hivatkozás(ok):	Feladatok: 2018/február: 2017. évi Kürschák matematikaverseny 1. feladata

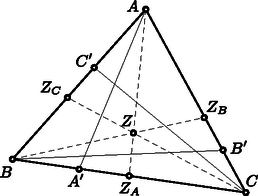
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek $Z_{A}$ , $Z_{B}$ és $Z_{C}$ rendre az $A Z$ , $B Z$ és $C Z$ egyenesek metszéspontjai az $A B C$ háromszög szemközti oldalával. Jelölje

\begin{matrix} α : = \frac{B Z_{A}}{B C}, β : = \frac{C Z_{B}}{C A} és γ : = \frac{A Z_{C}}{A B} \end{matrix}

azt, hogy ezek a pontok milyen arányban osztják az egyes oldalakat. Ekkor

\begin{matrix} \frac{Z_{A} C}{B C} = \frac{B C - B Z_{A}}{B C} = 1 - \frac{B Z_{A}}{B C} = 1 - α, \end{matrix}

és hasonlóan

\begin{matrix} \frac{Z_{B} A}{C A} = 1 - β, illetve \frac{Z_{C} B}{A B} = 1 - γ . \end{matrix}

A Ceva-tétel alapján

\begin{matrix} 1 & = \frac{B Z_{A}}{Z_{A} C} \cdot \frac{C Z_{B}}{Z_{B} A} \cdot \frac{A Z_{C}}{Z_{C} B} = \frac{B Z_{A}}{B C} \cdot \frac{B C}{Z_{A} C} \cdot \frac{C Z_{B}}{C A} \cdot \frac{C A}{Z_{B} A} \cdot \frac{A Z_{C}}{A B} \cdot \frac{A B}{Z_{C} B} = \\ = \frac{α β γ}{(1 - α) (1 - β) (1 - γ)} \end{matrix}

adódik, azaz

\begin{matrix} α β γ = (1 - α) (1 - β) (1 - γ) . \end{matrix}

(1)

Könnyen látható, hogy az

A A'

B B'

és

C C'

egyenesek által határolt (esetleg elfajuló) háromszög pontosan akkor tartalmazza a

Z

pontot, ha vagy

B A' \leq B Z_{A}

és

C B' \leq C Z_{B}

, valamint

A C' \leq A Z_{C}

teljesül; vagy akkor, ha

B A' \geq B Z_{A}

C B' \geq C Z_{B}

és

A C' \geq A Z_{C}

áll fenn. Ez azt jelenti, hogy

\begin{matrix} p (Z) = α β γ + (1 - α) (1 - β) (1 - γ) = 2 α β γ = 2 (1 - α) (1 - β) (1 - γ), \end{matrix}

az utóbbi egyenlőségek (1) miatt teljesülnek. A számtani és mértani közép közti egyenlőtlenségből

\begin{matrix} \sqrt[3]{\frac{p (Z)}{2}} & = \sqrt[3]{α β γ} \leq \frac{α + β + γ}{3}, illetve \\ \sqrt[3]{\frac{p (Z)}{2}} & = \sqrt[3]{(1 - α) (1 - β) (1 - γ)} \leq \frac{3 - α - β - γ}{3} \end{matrix}

következik, ahonnan

\begin{matrix} 2 \sqrt[3]{\frac{p (Z)}{2}} \leq \frac{α + β + γ}{3} + \frac{3 - α - β - γ}{3} = 1 \end{matrix}

alapján

p (Z) \leq \frac{1}{4}

adódik. Egyenlőség pedig akkor állhat, ha mindkét számtani és mértani közép közti egyenlőtlenségnél egyenlőség áll, azaz ha

α = β = γ

teljesül. Ekkor azonban (1) miatt

α = β = γ = \frac{1}{2}

, azaz

Z

A B C

háromszög súlypontja. Könnyen ellenőrizhető, hogy a súlypontra minden fenti becslés csakugyan egyenlőséggel teljesül. Ez pedig azt igazolja, hogy a feladat kérdésére a súlypont a válasz.

□

Megjegyzés. A feladat könnyen megoldható a baricentrikus koordináták segítségével. Legyenek tehát

α

β

γ

Z

baricentrikus koordinátái, azaz

\vec{Z} = α \vec{A} + β \vec{B} + γ \vec{C}

, ahol

\vec{X}

jelöli az

X

ponthoz tartozó helyvektort és

α + β + γ = 1

. Ekkor a

\begin{matrix} p (Z) = 2 \cdot \frac{α β γ}{(α + β) (β + γ) (γ + α)} \end{matrix}

kifejezést kell maximalizálni. Márpedig a számtani és mértani közép közti egyenlőtlenségből

\begin{matrix} (α + β) (β + γ) (γ + α) \geq 2 \sqrt[]{α β} \cdot 2 \sqrt[]{β γ} \cdot 2 \sqrt[]{γ α} = 8 α β γ \end{matrix}

adódik, ahonnan

\begin{matrix} p (Z) = 2 \cdot \frac{α β γ}{(α + β) (β + γ) (γ + α)} \leq 2 \cdot \frac{α β γ}{8 α β γ} = \frac{1}{4} \end{matrix}

következik, egyenlőség pedig kizárólag

α = β = γ

esetén áll. A kérdezett valószínűség tehát

α = β = γ = \frac{1}{3}

esetén, azaz a súlypontra maximális.