Feladat: B.4889 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Döbröntei Dávid Bence ,  Kerekes Anna 
Füzet: 2018/február, 91 - 92. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Beírt kör, Síkgeometriai bizonyítások, Párhuzamos szelők tétele és megfordítása
Hivatkozás(ok):Feladatok: 2017/szeptember: B.4889

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először lássunk be egy segédtételt. Használjuk az 1. ábra jelöléseit.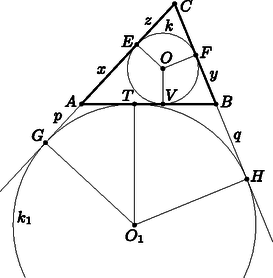


 

1. ábra
 

 
Tétel. A háromszög beírt és hozzáírt körének egy oldalra eső érintési pontjai szimmetrikusan helyezkednek el, tehát AT=VB.
 
Bizonyítás. Legyen a háromszög oldalainak hossza a szokásos jelölések szerint a, b, c, a beírt kör érintőszakaszainak hossza x, y, z, a hozzáírt kör érintőszakaszainak hossza p és q, a háromszög kerülete k, és s=k2.
CG=CH, mivel a k1 körhöz C pontból húzott érintőszakaszok.
CG+CH=CA+AT+TB+BC=k=2s, ezért CG=CH=s, amiből AT=p=s-b.
2x+2y+2z=k, vagyis x+y+z=s.
BV=y=s-(x+z)=s-b, tehát AT=BV.
Két esetre bontjuk a feladat bizonyítását.
1. eset: AB<CD. Használjuk a 2. ábra jelöléseit. Legyen k a beírt kör.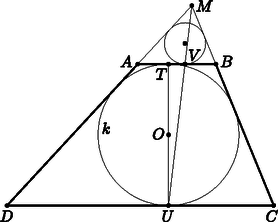


 

2. ábra
 

Ebben az esetben az M metszéspont az AB egyenes C és D pontokat nem tartalmazó oldalára esik. A k kör az MAB háromszög AB oldalához írt köre.
Nagyítsuk az ABM háromszöget az M pontból λ=MDMA arányban. Ekkor az MAB háromszög beírt köre k-ba megy át. Az AB egyenes képe a CD egyenes, hiszen AB∥CD és AB érinti a beírt kört, CD pedig érinti k-t. A V pont képe U lesz, hiszen a pont és a képe, valamint M egy egyenesen vannak, és V rajta van az AB egyenesen, így a képe rajta van a CD egyenesen. Tehát az AB egyenest az MAB háromszög beírt köre a V pontban érinti.
Használjuk a segédtételünket. A beírt kör érintési pontjának távolsága az egyik csúcstól egyenlő a hozzáírt kör távolságával a másik csúcstól, vagyis AT=VB.
2. eset: AB>CD. Használjuk a 3. ábra jelöléseit.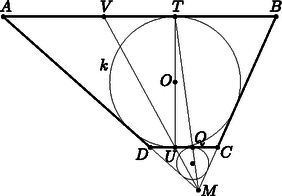


 

3. ábra
 

Most M a CD egyenes A és B pontot nem tartalmazó oldalán lesz. Ekkor k az MCD háromszög hozzáírt köre.
Nagyítsuk az MCD háromszöget az M pontból λ=MAMD arányban. Ekkor MCD beírt köre k-ba megy át. A CD egyenes képe az AB egyenes lesz. Mivel CD érinti a beírt kört, AB pedig érinti k-t, az U pont képe V, a Q pont képe pedig T lesz.
Pontosan akkor igaz, hogy AT=VB, ha DQ=CU. Utóbbi a segédtételünk értelmében igaz, így AT=VB is teljesül.
Ha AB=CD, akkor ABCD paralellogramma, azaz nem létezik az M pont.
 

 Kerekes Anna (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 11. évf.) és
 Döbröntei Dávid Bence (Pápa, Türr István Gimn. és Koll., 12 évf.)
 dolgozata alapján