Feladat:	5000. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Elek Péter ,  Olosz Adél
Füzet:	2018/május, 308 - 312. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Mágneses permeabilitás, Egyéb mágneses erőhatás
Hivatkozás(ok):	Feladatok: 2018/január: 5000. fizika feladat

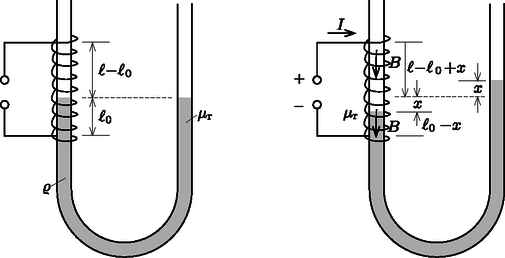
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Jelöljük az ábrán látható módon ${\ell }_0$-lal azt a távolságot, amennyire a víz ,,belóg'' a tekercsbe az áram bekapcsolása előtt, $x$-szel pedig azt, amennyivel lesüllyed a vízszint a tekercsben az áram bekapcsolása után.     A tekercsben (annak vízzel teli részében is és a levegőt tartalmazó részében is) $\begin{array}{c}{\displaystyle B\left(x\right)=\frac{NI{\mu }_0{\mu }_{\text{r}}}{\left(\ell -{\ell }_0+x\right){\mu }_{\text{r}}+\left({\ell }_0-x\right)}}\end{array}$ nagyságú mágneses indukció alakul ki (lásd az idézett cikket). Ez az indukció látható módon függ az $x$ távolságtól. A teljes ($A$ keresztmetszetű) tekercsen áthaladó mágneses fluxus: $\begin{array}{c}{\displaystyle \Phi \left(x\right)=NAB\left(x\right)\mathrm{,}}\end{array}$ ami ugyancsak $x$ függvénye. A fluxus kifejezhető a tekercs önindukciós együtthatójával is: $\begin{array}{c}{\displaystyle \Phi \left(x\right)=L\left(x\right)I\mathrm{.}}\end{array}$ Az áramjárta tekercs mágneses energiával rendelkezik, aminek nagysága $\begin{array}{c}{\displaystyle E_{\text{mágn.}}\left(x\right)=\frac{1}{2}LI{\left(x\right)}^2=\frac{1}{2}\Phi I=\frac{1}{2}ANI\cdot B\left(x\right)\mathrm{,}}\end{array}$ (1) vagyis $\begin{array}{c}{\displaystyle E_{\text{mágn.}}\left(x\right)=\frac{1}{2}\frac{N^2{I}^{2}A{\mu }_0{\mu }_{\text{r}}}{\left(\ell -{\ell }_0+x\right){\mu }_{\text{r}}+\left({\ell }_0-x\right)}\mathrm{.}}\end{array}$ (2) A folyadék gravitációs helyzeti energiája (az árammentes állapot azonos vízszintmagasságú állapotához viszonyítva) $\begin{array}{c}{\displaystyle E_{\text{helyzeti}}=\varrho gA{x}^2\mathrm{,}}\end{array}$ (3) hiszen $m=\varrho Ax$ tömegű folyadékmennyiség tömegközéppontja $x$-szel magasabbra került. Számítsuk most ki, hogy mennyit változna a rendszer mágneses, illetve gravitációs energiája, ha valamilyen ok miatt az $x$ távolság egy kicsiny $\Delta x\ll x$ értékkel növekedne. A (2) képletből közvetlen számolással adódik: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \Delta E_{\text{mágn.}}}& {\displaystyle =E_{\text{mágn.}}\left(x+\Delta x\right)-E_{\text{mágn.}}\left(x\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{N^2{I}^{2}A{\mu }_0{\mu }_{\text{r}}\left(1-{\mu }_{\text{r}}\right)\Delta x}{2\left[\left(\ell -{\ell }_0+x+\Delta x\right){\mu }_{\text{r}}+\left({\ell }_0-x-\Delta x\right)\right]\left[\left(\ell -{\ell }_0+x\right){\mu }_{\text{r}}+\left({\ell }_0-x\right)\right]}\approx }\hfill \\ \hfill {\displaystyle }& {\displaystyle \approx \frac{N^2{I}^{2}A{\mu }_0\left(1-{\mu }_{\text{r}}\right)\Delta x}{2{\ell }^2}\mathrm{.}}\hfill & \text{(<mn>4</mn>)}\end{array}}$ (Az utolsó lépésnél kihasználtuk, hogy $\Delta x\ll x$ és ${\mu }_{\text{r}}\approx 1$.) Ugyanezt az eredményt a differenciálszámítás alkalmazásával is megkaphatjuk: $\begin{array}{c}{\displaystyle \Delta E_{\text{mágn.}}\approx \frac{\text{d}{E}_{\text{mágn.}}\left(x\right)}{\text{d}x}\cdot \Delta x\mathrm{.}}\end{array}$ Mivel víznél ${\mu }_{\text{r}}<1$ (a víz diamágneses), (4)-ből leolvasható, hogy a vízszint kicsiny lesüllyedésekor (vagyis $\Delta x>0$ esetén) a rendszer mágneses energiája növekszik. Hasonló módon számíthatjuk ki a (3)-ból, hogy mennyit változna a víz helyzeti energiája, ha a vízszint valamilyen ok miatt egy kicsiny $\Delta x$ értékkel lesüllyedne: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle \Delta E_{\text{helyzeti}}}& {\displaystyle =E_{\text{helyzeti}}\left(x+\Delta x\right)-E_{\text{helyzeti}}\left(x\right)=}\hfill & \text{(<mn>5</mn>)}\\ \hfill {\displaystyle }& {\displaystyle =\varrho gA\Delta x\left(2x+\Delta x\right)\approx 2\varrho gAx\cdot \Delta x\mathrm{,}}\hfill \end{array}}$ ami így is megkapható: $\begin{array}{c}{\displaystyle \Delta E_{\text{helyzeti}}\approx \frac{\text{d}{E}_{\text{helyzeti}}\left(x\right)}{\text{d}x}\cdot \Delta x\mathrm{.}}\end{array}$ Látható, hogy $x>0$ és $\Delta x>0$ esetén a folyadék helyzeti energiája is növekszik. Vajon mi fedezné a rendszer mágneses és gravitációs helyzeti energiájának megváltozását, ha a vízszint $\Delta x$ értékkel lesüllyedne? A vízszint elképzelt változásakor a tekercsen áthaladó mágneses fluxus $\begin{array}{c}{\displaystyle \Delta \Phi =I\Delta L}\end{array}$ értékkel megváltozik, miközben az áramforrás (áramgenerátor) biztosítja, hogy az $I$ áramerősség változatlan maradjon. A fluxusváltozás feszültséget indukál a tekercsben, emiatt az áramforrás feszültségének is meg kell növekednie $\begin{array}{c}{\displaystyle U=\frac{\Delta \Phi }{\Delta t}}\end{array}$ értékkel (ahol $\Delta t$ az elképzelt változás ideje). Ilyen körülmények között az áramforrás több energiát ad le, mint amennyit korábban (a Joule-hő fedezésére) leadott, a különbség $\begin{array}{c}{\displaystyle W=UI\Delta t=\frac{\Delta \Phi }{\Delta t}I\Delta t=I\Delta \Phi \mathrm{.}}\end{array}$ (6) (6) és (1) összevetéséből látszik, hogy $W=2\Delta E_{\text{mágn.}}$. Egyensúly esetén az elképzelt (virtuális) vízszintváltozásnál teljesülnie kell a $\begin{array}{c}{\displaystyle W=\Delta E_{\text{mágn.}}+\Delta E_{\text{helyzeti}}}\end{array}$ összefüggésnek. Ha a fenti összefüggés nem állna fenn, akkor valamilyen előjelű $\Delta x$ mellett $W$ nagyobb lenne, mint a rendszer mágneses és gravitációs energiájának megváltozása. A különbség fedezhetné a folyadék mozgási energiáját, és így a folyadék nem maradna egyensúlyban, hanem mozgásba jönne. Az egyensúly feltétele tehát $\begin{array}{c}{\displaystyle W=2\Delta E_{\text{mágn.}}=\Delta E_{\text{mágn.}}+\Delta E_{\text{helyzeti}}\mathrm{,}}\end{array}$ ami (4) és (5) felhasználásával így írható: $\begin{array}{c}{\displaystyle \frac{N^2{I}^{2}A{\mu }_0\left(1-{\mu }_{\text{r}}\right)\Delta x}{2{\ell }^2}=2\varrho gAx\cdot \Delta x\mathrm{.}}\end{array}$ Innen a vízszint keresett megváltozása az áram hatására: $\begin{array}{c}{\displaystyle x=\frac{N^2{I}^2{\mu }_0\left(1-{\mu }_{\text{r}}\right)}{4{\ell }^2\varrho g}\mathrm{.}}\end{array}$ Mivel $x>0$, a víz a tekercs belsejében egy kicsit lesüllyed.    Olosz Adél (Pécs, PTE. Gyak. Ált. Isk., Gimn. és Szakgimn., 11. évf.)  dolgozata alapján     II. megoldás. A vízszint mágneses mező okozta eltolódását a mágneses indukció nagysága határozza meg, és a vízszint egyensúlyi helyzete nem függ attól, hogy mi hozza létre a mágneses mezőt. Cseréljük fel a feladatban szereplő tekercset egy ugyanolyan geometriájú, rövidre zárt szupravezető tekerccsel, amiben ugyancsak $I$ erősségű áram folyik az egyensúlyi állapotban. Ez a rendszer energetikailag zárt (hiszen nem kapcsolódik külső áramforráshoz), ezért az egyensúlyi állapotát az összes (mágneses + gravitációs) energia minimuma határozza meg. A folyadék gravitációs helyzeti energiája (az I. megoldás jelöléseit használva) $\begin{array}{c}{\displaystyle E_{\text{helyzeti}}\left(x\right)=\varrho gA{x}^2\mathrm{.}}\end{array}$ A tekercs belsejében $\begin{array}{c}{\displaystyle B={\mu }_0\frac{NI}{\ell }}\end{array}$ (7) indukciójú mágneses mező van, hiszen mind a levegő, mind pedig a víz relatív permeabilitása jó közelítéssel 1-nek tekinthető. A mágneses tér energiája az energiasűrűség $B^2/\left(2{\mu }_0{\mu }_{\text{r}}\right)$ képletből számolható. Mivel a tekercs ${\ell }_0-x$ hosszú részét víz, $\ell -{\ell }_0+x$ hosszú részét pedig levegő tölti ki, a mágneses energia: $\begin{array}{c}{\displaystyle E_{\text{mágn.}}\left(x\right)=\frac{B^{2}A}{2{\mu }_0}\left(\frac{{\ell }_0-x}{{\mu }_{\text{r}}^{\text{(víz)}}}+\frac{\ell -{\ell }_0+x}{{\mu }_{\text{r}}^{\text{(levegő)}}}\right)\mathrm{.}}\end{array}$ Ebben a kifejezésben $B$ a (7) összefüggéssel megadott mágneses indukció, ami szupravezető tekercs esetében (a mágneses fluxus állandósága miatt) nem függ $x$-től. A rendszer teljes energiája $\begin{array}{c}{\displaystyle E\left(x\right)=E_{\text{helyzeti}}\left(x\right)+E_{\text{mágn.}}\left(x\right)=\varrho gA{x}^2+{\mu }_0\frac{N^2{I}^{2}A}{2{\ell }^2}\left(\frac{{\ell }_0-x}{{\mu }_{\text{r}}^{\text{(víz)}}}+\frac{\ell -{\ell }_0+x}{{\mu }_{\text{r}}^{\text{(levegő)}}}\right)\mathrm{.}}\end{array}$ Ez $x$-ben másodfokú kifejezés, aminek minimumát pl. teljes négyzetté alakítással, a parabola tulajdonságainak felhasználásával, esetleg deriválással határozhatjuk meg: $\begin{array}{c}{\displaystyle x={\mu }_0\frac{N^2{I}^2\left({\mu }_{\text{r}}^{\text{(levegő)}}-{\mu }_{\text{r}}^{\text{(víz)}}\right)}{4{\ell }^2\varrho g{\mu }_{\text{r}}^{\text{(víz)}}{\mu }_{\text{r}}^{\text{(levegő)}}}\approx {\mu }_0\frac{N^2{I}^2\left(1-{\mu }_{\text{r}}\right)}{4{\ell }^2\varrho g}\mathrm{,}}\end{array}$ ahol ${\mu }_{\text{r}}=0\mathrm{,}999992$ a víz relatív permeabilitása, a levegő 1,000 000 36 értékű relatív permeabilitását pedig 1-gyel helyettesítettük.    Elek Péter (Debreceni Ref. Koll. Dóczy Gimn., 11. évf.)  dolgozata alapján