Kezdőlap


Feladat:	B.4836	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	2018/január, 21 - 22. oldal		PDF \| MathML
Témakör(ök):	Feladat, Terület, felszín, Körülírt kör, Szögfelező egyenes
Hivatkozás(ok):	Feladatok: 2016/december: B.4836

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Húzzunk párhuzamost az $M$ ponton keresztül az $A B$ oldallal, ez az egyenes messe a $B C$ és $A D$ egyeneseket rendre a $C^{*}$ és $D^{*}$ pontokban. Legyen $M A D^{*} ∢ = M A B ∢ = α$ és $M B A ∢ = M B C^{*} ∢ = β$ . Vegyük észre, hogy $A M D^{*} = M A B ∢ = α$ , hiszen váltószögek, és hasonlóan $B M C^{*} ∢ = M B A ∢ = β$ . Így az $A M D^{*} ▵$ és az $M B C^{*} ▵$ egyenlő szárú, amiből $M D^{*} = D^{*} A = C^{*} B = M C^{*} = A B / 2$ adódik, ahol a második egyenlőségnél kihasználtuk, hogy $A B C^{*} D^{*}$ paralelogramma, az utolsó egyenlőségnél pedig, hogy 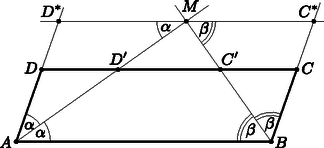$M D^{*} + M C^{*} = D^{*} C^{*} = A B$ .

Feltehetjük, hogy

T_{A B C^{*} D^{*}} = 2

. Mivel az

A B C^{*} D^{*}

paralelogramma és az

A B M ▵

A B

oldala és ehhez tartozó magassága közös, a jól ismert területképletek alapján

T_{A B M} = 1

. Továbbá a feltétel szerint

A D = λ A B = 2 λ A D^{*}

, így ismét a paralelogramma ismert területképlete szerint

\begin{matrix} T_{A B C D} = A B \cdot A D \cdot sin 2 α = 2 λ (A B \cdot A D^{*} \cdot sin 2 α) = 2 λ T_{A B C^{*} D^{*}} = 4 λ . \end{matrix}

Az eddigiekből az is következik, hogy az

M

pont pontosan akkor van benne az

A B C D

paralelogrammában, ha

λ \geq 1 / 2

. Ilyenkor a keresett területarány a fentiekből azonnal adódik:

\begin{matrix} \frac{T_{A B M}}{T_{A B C D}} = \frac{1}{4 λ} . \end{matrix}

λ < 1 / 2

, akkor az

M

pont

A B C D

-n kívül esik. Messe

A M

és

B M

C D

oldalt rendre a

D'

és

C'

pontokban. Ekkor a

D^{*} A M ∢

-ben a párhuzamos szelők tétele szerint

\begin{matrix} \frac{A D'}{A M} = \frac{A D}{A D^{*}} = 2 λ . \end{matrix}

Világos, hogy

M D' C' ▵ \sim M A B ▵

, hiszen szögeik páronként megegyeznek, és hasonlóságuk aránya

M D' / M A = 1 - D A' / M A = 1 - 2 λ

. Ebből következik, hogy

T_{M D' C'} = {(1 - 2 λ)}^{2} T_{M A B} = {(1 - 2 λ)}^{2}

. Végül az

A B M ▵

által lefedett területre

\begin{matrix} T_{A B C' D'} = T_{A B M} - T_{M C' D'} = 1 - {(1 - 2 λ)}^{2} = 4 λ - 4 λ^{2} . \end{matrix}

Innen pedig

\begin{matrix} \frac{T_{A B C' D'}}{T_{A B C D}} = \frac{4 λ - 4 λ^{2}}{4 λ} = 1 - λ . \end{matrix}

Tehát a keresett arány

1 / 4 λ

, ha

λ \geq 1 / 2

; és

1 - λ

, ha

λ < 1 / 2