Kezdőlap


Feladat:	4977. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Tófalusi Ádám
Füzet:	2018/április, 248 - 249. oldal		PDF \| MathML
Témakör(ök):	Feladat, Egyéb áramkörök
Hivatkozás(ok):	Feladatok: 2017/november: 4977. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A kapcsoló zárása előtt a töltetlen kondenzátorok feszültsége nyilván nulla. A kapcsoló zárásakor a kondenzátorok ,,rövidre zárják'' az áramforrást, és ‐ ha a feladat szövegében szereplő közelítésekkel élünk ‐ egy ,,pillanat alatt'' feltöltődnek. A kondenzátorok közös pontjára csak az ellenállásokon keresztül juthat töltés, így az össztöltésük hirtelen nem tud megváltozni, tehát a két kondenzátor (egy nagyon rövid ideig) sorosan kapcsoltnak tekinthető. A hirtelen feltöltődött kondenzátorok kezdeti feszültsége a kapacitások reciprokának arányában megosztott telepfeszültség:

\begin{matrix} \frac{U_{1,0}}{U_{2,0}} = \frac{C_{2}}{C_{1}} = \frac{1}{3}, U_{1,0} + U_{2,0} = U_{0} = 100 V, \end{matrix}

vagyis

\begin{matrix} U_{1,0} = 25 V és U_{2,0} = 75 V . \end{matrix}

A kapcsoló zárása után elegendően hosszú (,,végtelen hosszú'') idővel a kondenzátorok töltése már nem változik, a feszültségük tehát valamekkora állandósult

U_{1, \infty}

és

U_{2, \infty}

értékre áll be. Ilyenkor az ellenállások közös pontját a kondenzátorok közös pontjával összekötő vezetéken már nem folyik áram, tehát mindkét ellenálláson ugyanakkora áram folyik.
Az ellenállásokra eső feszültség (ami megegyezik a kondenzátorokra eső feszültséggel) az ellenállások arányában osztja meg az áramforrás feszültségét:

\begin{matrix} \frac{U_{1, \infty}}{U_{2, \infty}} = \frac{R_{1}}{R_{2}} = 4, U_{1, \infty} + U_{2, \infty} = U_{0} = 100 V, \end{matrix}

vagyis

\begin{matrix} U_{1, \infty} = 80 V és U_{2, \infty} = 20 V . \end{matrix}

A kondenzátorok feszültségének időbeli változása várhatóan exponenciális függvénnyel írható le. Ezen sejtés szigorú bizonyításához a változásokat megadó differenciálegyenleteket kellene felírnunk és megoldanunk. Szerencsére ennél sokkal egyszerűbben is eljárhatunk. A töltések átrendeződése, azok időbeli változása ugyanolyan jellegű, ugyanolyan ,,időállandójú'' exponenciális függvényekkel írható le a kondenzátorok feltöltődésekor is, mint a kisülésükkor (lásd pl. a Kondenzátor feltöltése és kisülése ohmos ellenálláson át című részt a ,,Függvénytáblázat'' 148. oldalán).
Ha az áramforrást (zárt kapcsolóállás mellett) kiiktatjuk az áramkörből és az eredetileg hozzá csatlakozó vezetékeket rövidre zárjuk, akkor egy olyan kapcsoláshoz jutunk, amelyben két párhuzamosan kapcsolt, tehát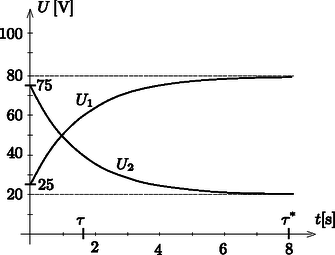

\begin{matrix} C_{e} = C_{1} + C_{1} = 200 μ F \end{matrix}

eredő kapacitású kondenzátor két párhuzamosan kapcsolt, tehát

\begin{matrix} R_{e} = \frac{R_{1} R_{2}}{R_{1} + R_{2}} = 8 kΩ \end{matrix}

eredő ellenálláson keresztül veszíti el töltését. A kisülés folyamata időben exponenciálisan,

e^{- t / τ}

függvénnyel leírható módon zajlik le, ahol az időállandó

\begin{matrix} τ = R_{e} C_{e} = (8 \cdot 10^{3} Ω) (2 \cdot 10^{- 4} F) = 1, 6 s. \end{matrix}

Megjegyzés. Simonyi Károly Villamosságtan című könyvében említi, hogy a feszültség beállásának idejét

τ^{*} = 5 τ

idővel szokták közelíteni. Esetünkben a kondenzátorok feszültsége 8 s alatt változik meg a kezdeti értékekről a végső (aszimptotikus) értékekre, ahogy azt az ábra mutatja.

Tófalusi Ádám (Debreceni Fazekas M. Gimn., 11. évf.)
dolgozata alapján