Feladat:	4975. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gnädig Péter ,  Illés Gergely ,  Tófalusi Ádám
Füzet:	2018/április, 240 - 245. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Mozgás homogén mágneses mezőben
Hivatkozás(ok):	Feladatok: 2017/november: 4975. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.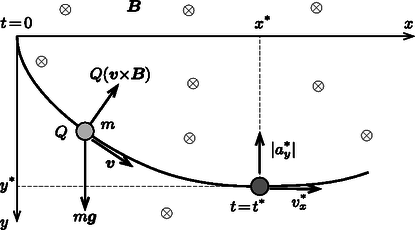   I. megoldás. Vegyünk fel egy olyan koordináta-rendszert, amelynek $x$ tengelye vízszintes, $y$ tengelye pedig függőlegesen lefelé mutat. A mágneses indukció ugyancsak vízszintes irányú és az ábrán látható módon a papír síkjába befelé irányul. A kicsiny töltött test a koordináta-rendszer origójából indul, és a pályája ‐ vázlatosan ‐ az ábrán látható görbe. (A mozgás nyilván az $x-y$ síkban történik, így elegendő ezt vizsgálnunk.)     A ,,földi laboratórium'' kifejezés arra utal, hogy a testre ható erők között a mágneses Lorentz-erő mellett a nehézségi erőt is figyelembe kell vennünk. A testre ható erő komponensei: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle F_x}& {\displaystyle =Q{v}_{y}B\mathrm{,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle F_y}& {\displaystyle =mg-Q{v}_{x}B\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\end{array}}$ ahol $\begin{array}{c}{\displaystyle v_x=\frac{\Delta x\left(t\right)}{\Delta t}\text{és}{v}_y=\frac{\Delta y\left(t\right)}{\Delta t}}\end{array}$ (3) a test sebességének megfelelő derékszögű összetevői. A Newton-féle mozgásegyenletek: $\begin{array}{c}{\displaystyle F_x=m{a}_x\text{és}{F}_y=m{a}_y\mathrm{,}}\end{array}$ ahol $\begin{array}{c}{\displaystyle a_x=\frac{\Delta v_x\left(t\right)}{\Delta t}\text{és}{y}_y=\frac{\Delta v_y\left(t\right)}{\Delta t}\mathrm{.}}\end{array}$ (4) Behelyettesítve az erőkomponenseket a következő mozgásegyenleteket kapjuk: $\begin{array}{c}{\displaystyle a_x={\omega }_0{v}_y\mathrm{,}}\end{array}$ (5) és $\begin{array}{c}{\displaystyle a_y=g-{\omega }_0{v}_x\mathrm{,}}\end{array}$ (6) ahol $\begin{array}{c}{\displaystyle {\omega }_0=\frac{QB}{m}}\end{array}$ (7) egy körfrekvencia dimenziójú állandó.   Megjegyzés. Ezt a mennyiséget ,,ciklotronfrekvenciának'' nevezik, mert ilyen körfrekvenciával mozog a ciklotronokban egy $Q/m$ fajlagos töltésű részecske a $B$ indukciójú homogén mágneses mezőben.   Felírhatjuk még a munkatételt a töltött részecske mozgására az indulás pillanata és egy tetszőleges későbbi pillanat között. Mivel a Lorentz-erő merőleges a sebességre, tehát nem végez munkát, elegendő a nehézségi erő munkavégzésével számolnunk: $\begin{array}{c}{\displaystyle \frac{1}{2}m\left(v_x{\left(t\right)}^2+v_y{\left(t\right)}^2\right)=mgy\left(t\right)\mathrm{.}}\end{array}$ (8) Innen leolvashatjuk, hogy a test sebessége akkor lesz a legnagyobb, amikor a függőleges elmozdulás ($y^{*}$) maximális. Mivel ilyenkor a függőleges irányú sebesség éppen nulla, a vízszintes irányú sebességkomponensre fennáll: $\begin{array}{c}{\displaystyle v_x^{*}=\sqrt[]{2g{y}^{*}}\mathrm{.}}\end{array}$ (9) $a)$ és $b)$ Írjuk fel az (5) egyenletet a kicsiny sebesség- és elmozdulás-megváltozásokkal, majd összegezzük ezeket a megváltozásokat a mozgás kezdetétől a pálya legmélyebb pontjáig: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{\Delta v_x\left(t\right)}{\Delta t}={\omega }_0\frac{\Delta y\left(t\right)}{\Delta t}\mathrm{,}}\hfill \\ \hfill {\displaystyle \sum \Delta v_x\left(t\right)={\omega }_0\sum \Delta y\left(t\right)\mathrm{,}}\hfill \end{array}}$ ahonnan $\begin{array}{c}{\displaystyle v_x^{*}={\omega }_0{y}^{*}}\end{array}$ (10) adódik. Összevetve ezt az eredményt a munkatételből kapott (9) összefüggéssel, válaszolhatunk az első két alkérdésre. A test legnagyobb sebessége $\begin{array}{c}{\displaystyle |\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}|=v_x^{*}=\frac{2g}{{\omega }_0}=\frac{2mg}{QB}\mathrm{,}}\end{array}$ a legmélyebb süllyedése pedig (az indulási magassághoz viszonyítva): $\begin{array}{c}{\displaystyle y^{*}=\frac{2g}{{\omega }_0^2}=\frac{2g{m}^2}{Q^2{B}^2}\mathrm{.}}\end{array}$ $c)$ A fentiekhez hasonló módon járhatunk el a vízszintes irányú (6) mozgásegyenlettel, ami $\begin{array}{c}{\displaystyle \Delta v_y\left(t\right)=g\Delta t-{\omega }_0\Delta x\left(t\right)}\end{array}$ alakban is felírható. Összegezve a mozgás kezdetétől a legmélyebb pontba érkezés $t^{*}$ időpillanatáig, amikor a vízszintes irányú elmozdulás $x^{*}$, a függőleges irányú sebesség pedig nulla: $\begin{array}{c}{\displaystyle 0=g{t}^{*}-{\omega }_0{x}^{*}\mathrm{,}}\end{array}$ ahonnan a mozgás ezen szakaszára vonatkoztatott átlagsebesség: $\begin{array}{c}{\displaystyle \overline{v}=\frac{x^{*}}{t^{*}}=\frac{g}{{\omega }_0}=\frac{mg}{QB}\mathrm{.}}\end{array}$ Mivel a vízszintes irányú mozgás a $0<x\left(t\right)<x^{*}$ intervallumon történő mozgás ismétlődése, az egész mozgás átlagsebessége ($x^{*}$-nál sokkal hosszabb úton) ugyancsak $mg/\left(QB\right)$. $d)$ A pálya legmélyebb pontjánál a test gyorsulása (6) szerint: $\begin{array}{c}{\displaystyle a_y^{*}=g-{\omega }_0{v}_x^{*}\mathrm{,}}\end{array}$ ami (7) és a $v_x^{*}$-re kapott kifejezés alapján: $\begin{array}{c}{\displaystyle a_y^{*}=g-\frac{QB}{m}\frac{2mg}{QB}=g-2g=-g\mathrm{.}}\end{array}$ A töltött test tehát éppen a nehézségi gyorsulással megegyezően gyorsul függőlegesen felfelé.    Illés Gergely (Eger, Szilágyi Erzsébet Gimn., 12. évf.)  dolgozata alapján     II. megoldás. Tekintsünk egy olyan koordináta-rendszert, amely az indukcióvonalakra merőlegesen, vízszintes irányban ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}}_0$ sebességgel mozog a laboratóriumi rendszerhez képest. Ha a töltött test pillanatnyi sebessége a ,,mozgó'' rendszerben $\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}$, akkor a laboratóriumi rendszerben a sebessége $\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}+{\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}}_0$, így a Newton-féle mozgásegyenlet: $\begin{array}{c}{\displaystyle m\text{<span style="font-weight: bold;"><span style="font-style: italic;">a</span></span>}=Q\left(\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}+{\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}}_0\right)\times \text{<span style="font-weight: bold;"><span style="font-style: italic;">B</span></span>}+m\text{<span style="font-weight: bold;"><span style="font-style: italic;">g</span></span>}\mathrm{,}}\end{array}$ amit $\begin{array}{c}{\displaystyle m\text{<span style="font-weight: bold;"><span style="font-style: italic;">a</span></span>}=Q\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}\times \text{<span style="font-weight: bold;"><span style="font-style: italic;">B</span></span>}+\left[m\text{<span style="font-weight: bold;"><span style="font-style: italic;">g</span></span>}+Q{\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}}_0\times \text{<span style="font-weight: bold;"><span style="font-style: italic;">B</span></span>}\right]}\end{array}$ (11) alakban is felírhatunk. A fenti képletben $\text{<span style="font-weight: bold;"><span style="font-style: italic;">a</span></span>}$ a test gyorsulása, ami a laboratóriumi rendszerben ugyanaz a vektor, mint az egyenletesen mozgó másik koordináta-rendszerben a gyorsulás. A (11) egyenlet szögletes zárójelében szereplő két vektor ugyanolyan (függőleges) irányú, és ha ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}}_0$ nagyságát megfelelően, nevezetesen $v_0=mg/\left(QB\right)$ módon választjuk, a két tag éppen kiejtheti egymást. Ekkor a mozgásegyenlet olyan, mintha a test súlytalan lenne, és csak a mágneses Lorentz-erő hatása alatt mozogna. Úgy is mondhatjuk, hogy a mozgó rendszerben megjelenik egy $E=B{v}_0$ nagyságú homogén, függőlegesen felfelé irányuló elektromos mező, aminek hatása kiegyenlíti az $mg$ nagyságú, függőlegesen lefelé mutató nehézségi erőt. Jól ismert, hogy homogén mágneses mezőben a mágneses erővonalakra merőleges kezdősebességgel rendelkező részecske pályája kör, és a részecske a kör mentén ${\omega }_0=QB/m$ körfrekvenciával egyenletesen mozog. Jelen esetben is ez valósul meg, hiszen a test kezdősebessége a laboratóriumi rendszerben nulla, a mozgó rendszerben tehát $v_0$ nagyságú. A körpálya sugara $\begin{array}{c}{\displaystyle R=\frac{v_0}{{\omega }_0}={\left(\frac{m}{QB}\right)}^{2}g}\end{array}$ lesz. A mozgás ‐ a laboratóriumi rendszerből nézve ‐ egy $v_0$ sebességű egyenletes mozgás és egy $v_0$ kerületi sebességű körmozgás szuperpozíciója. A pálya alakja ezek szerint ciklois. $a)$ A test sebessége a pálya legmélyebb pontjánál lesz a legnagyobb, ugyanis itt lesz egymással párhuzamos és egyirányú a kétféle mozgáshoz tartozó sebességvektor: $\begin{array}{c}{\displaystyle v_{\text{max}}=2v_0=2\frac{mg}{QB}\mathrm{.}}\end{array}$ $b)$ A test legnagyobb lesüllyedése a kezdőponthoz képest $\begin{array}{c}{\displaystyle \Delta h=2R=2{\left(\frac{m}{QB}\right)}^{2}g\mathrm{.}}\end{array}$ $c)$ A test sebessége a vízszintes irányú, állandó $v_0$ nagyságú sebességnek és a körmozgásból adódó, a nulla körül ingadozó sebességnek a vektori összege. Az eredő (hosszú időtartamra vonatkoztatott) átlagsebesség tehát $v_0$ nagyságú, vízszintes és a mágneses erővonalakra is merőleges irányú vektor lesz. $d)$ A test gyorsulása csak a körmozgásból adódik, nagysága a pálya minden pontjában $\begin{array}{c}{\displaystyle a=\frac{v_0^2}{R}={\left(\frac{mg}{QB}\right)}^2\cdot {\left(\frac{QB}{m}\right)}^2\frac{1}{g}=g}\end{array}$ nagyságú. A gyorsulás iránya a mozgás kezdetekor függőlegesen lefelé, a pálya legmélyebb pontjában pedig függőlegesen felfelé mutat.    Tófalusi Ádám (Debreceni Fazekas M. Gimn., 11. évf.)  dolgozata alapján   III. megoldás. Használjuk az I. megoldás jelöléseit, és induljunk ki a vízszintes és a függőleges irányokra vonatkozó (5) és (6) mozgásegyenletből. Az (5) egyenlet, amit $a_x-{\omega }_0{v}_y=0$ alakban is felírhatunk, azt fejezi ki, hogy a $v_x\left(t\right)-{\omega }_{0}y\left(t\right)$ mennyiség változási üteme (deriváltja) nulla, tehát ez a kifejezés időben állandó. Az állandó (mivel a kezdőpillanatban $v_x$ is és $y$ is nulla) nulla kell hogy legyen, vagyis $\begin{array}{c}{\displaystyle v_x\left(t\right)={\omega }_{0}y\left(t\right)\mathrm{.}}\end{array}$ (12) Helyettesítsük be $v_x$-et a függőleges irányú mozgásra vonatkozó (6) egyenletbe: $\begin{array}{c}{\displaystyle a_y\left(t\right)=g-{\omega }_0^{2}y\left(t\right)\mathrm{,}}\end{array}$ amit $\begin{array}{c}{\displaystyle a_y\left(t\right)=-{\omega }_0^2\left(y\left(t\right)-y_0\right)}\end{array}$ (13) alakban is felírhatunk, ahol $y_0=g/{\omega }_0^2$. Felismerhetjük, hogy (13) egy olyan rugóra akasztott súlyos test mozgásegyenlete, amely test saját súlya alatt a rugó megnyúlása $y_0$, és a rezgés körfrekvenciája ${\omega }_0$. A harmonikus rezgőmozgás ismert képleteiből (az $y\left(0\right)=0$ és $v_y\left(0\right)=0$ kezdőfeltételeket is figyelembe véve) könnyen megkaphatjuk, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y\left(t\right)}& {\displaystyle =\frac{g}{{\omega }_0^2}\left(1-\text{cos}{\omega }_{0}t\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle v_y\left(t\right)}& {\displaystyle =\frac{g}{{\omega }_0}\text{sin}{\omega }_{0}t\mathrm{,}}\hfill \\ \hfill {\displaystyle a_y\left(t\right)}& {\displaystyle =g\text{cos}{\omega }_{0}t\mathrm{.}}\hfill \end{array}}$ Ezekből (12) segítségével rögtön adódik, hogy $\begin{array}{c}{\displaystyle v_x\left(t\right)=\frac{g}{{\omega }_0}\left(1-\text{cos}{\omega }_{0}t\right)\mathrm{,}}\end{array}$ ennek változási üteme pedig $\begin{array}{c}{\displaystyle a_x\left(t\right)=g\text{sin}{\omega }_{0}t\mathrm{.}}\end{array}$ Az $x\left(t\right)$-t úgy kapjuk meg, hogy olyan függvényt keresünk, aminek változási üteme $v_x\left(t\right)$, és a kezdőpillanatban nulla értékű: $\begin{array}{c}{\displaystyle x\left(t\right)=\frac{g}{{\omega }_0^2}\left({\omega }_{0}t-\text{sin}{\omega }_{0}t\right)\mathrm{.}}\end{array}$ A fenti képletekből a feladat valamennyi kérdésére könnyen megkapjuk a választ: a test legnagyobb sebessége $2g/{\omega }_0$, legnagyobb lesüllyedése $2g/{\omega }_0^2$, a mozgás átlagsebessége $g/{\omega }_0$, és a gyorsulása a pálya legalsó pontjában (és minden más helyes is) $g$.   Megjegyzés. Mindhárom megoldásban a newtoni mechanika nemrelativisztikus mozgásegyenletéből indultunk ki. Ez csak akkor jogos, ha $v_{\text{max}}\ll c$, vagyis $mg\ll QBc$. Ez sokkal erősebb megszorítás, mint a feladat szövegében szereplő $mg<QBc$.    (G. P.)