| Feladat: | 4969. fizika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Elek Péter , Marozsák Tóbiás , Olosz Adél , Tófalusi Ádám | ||
| Füzet: | 2018/március, 181 - 186. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Feladat, Áramvezetőre ható erő | ||
| Hivatkozás(ok): | Feladatok: 2017/október: 4969. fizika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A két tekercs között ható erő vonzó hatású, ha a két áram ( és ) körüljárási iránya megegyezik, ellenkező esetben pedig ugyanakkora nagyságú, de taszító. A továbbiakban három különböző megoldást mutatunk a feladatra. A nagy tekercs által a kis tekercs helyén létrehozott mágneses térnek tengelyirányú komponense, illetve radiálisan kifelé mutató komponense van (1. ábra). Vegyük észre, hogy a képlet szerint tengelyirányú erőt csak okoz, azaz feladatunk ennek a komponensnek a meghatározása. 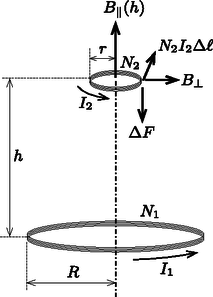 1. ábra Ismeretes, de a Biot‐Savart-törvény segítségével könnyen le is vezethető (ettől itt most eltekintünk), hogy a nagy tekercs által a tengely mentén, a tekercs középpontjától távolságban keltett mágneses indukció nagysága Vegyünk fel egy igen kicsiny magasságú, sugarú hengerfelületet (koaxiálisan) a kis tekercs köré (2. ábra). Tekintettel arra, hogy és , a mágneses indukció nagysága a henger alap- és fedőlapján, illetve az oldalpalást mentén állandónak vehető. A henger felső lapján a mágneses indukció nagysága egy kicsiny -vel különbözik az alaplap menti indukciótól: 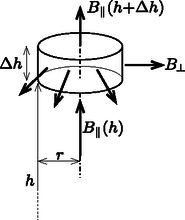 2. ábra A kis tekercsre ható eredő erő (kihasználva, hogy a tekercs minden pontjában merőleges -re): Minthogy , a kis tekercs mágneses tere közelíthető egy Bontsuk fel az vektort két komponensre a 3. ábrán látható módon. Az egyes komponensek által létrehozott mágneses indukcióvektorok nagyságát (, illetve ) és irányát könnyen meghatározhatjuk a dipólustól távol lévő pontban, hiszen ezek a Gauss-féle főhelyzeteknek felelnek meg. nagysága az I. Gauss-féle főhelyzetre (a dipól tengelyére eső pontokra) vonatkozó ismert képlet (lásd az I. megoldást) alapján: nagysága a II. Gauss-féle főhelyzetre (a dipól tengelyére merőleges síkban elhelyezkedő pontokra) vonatkozó képlet alapján: 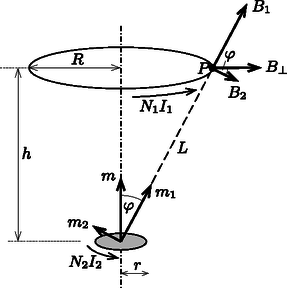 3. ábra 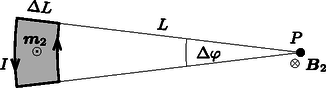 4. ábra A 3. ábra alapján a keresett radiális indukciókomponens nagysága A két lapos tekercs kölcsönös indukciós együtthatóját könnyen meghatározhatjuk, ha a nagy tekercs által létrehozott mágneses indukcióvektort a kis tekercs által határolt körlapon állandónak tekintjük. (Ez a feltevés miatt jogos.) A kis tekercsen áthaladó mágneses fluxus: A rendszer mágneses terének energiáját az A hiba forrása a következő: miközben a tekercseket eltávolítjuk egymástól, a bennük folyó áramot csak külső feszültségforrások segítségével tarthatjuk állandó értéken, és ezen feszültségforrások által leadott energiát nem vettük figyelembe az energiamérleg felírásánál. Ha a munkatételt helyesen akarjuk alkalmazni, akkor vagy ki kell számítanunk a külső áramforrások energialeadását, vagy ‐ egy ,,trükk'' alkalmazásával ‐ energetikailag zárttá kell tennünk a rendszert. A továbbiakban a második módszert követjük. A tekercseket, amelyekben kezdetben és áram folyt, oly mértékben lehűthetjük, hogy szupravezetőkké váljanak. Ekkor az áramok fenntartásához nincs szükség külső feszültségforrásra, tehát a tekercsek kivezetéseit akár rövidre is zárhatjuk. A tekercsek között ható erő nyilván csak az áramok nagyságától függ, attól nem, hogy milyen hőmérsékletűek (milyen vezetőképességűek) a vezetékek. Távolítsuk el gondolatban a két lehűtött (szupravezetővé tett) tekercset egymástól egy kicsiny távolsággal. A rendszer most energetikailag zárt, tehát az általunk végzett munka a mágneses energia megváltozásával lesz egyenlő. Mivel a szupravezető tekercsek mágneses fluxusa nem változhat meg (ellenkező esetben feszültség indukálódna, és az ,,végtelen nagy'' áramot indítana el bennük), a tekercsek eltávolítása közben nemcsak , hanem és is változni fog. A tekercsek fluxusa, vagyis A kölcsönös indukciós együttható kicsiny megváltozását az I. megoldásban alkalmazott módon (differenciálszámítással, vagy a Newton-formula alkalmazásával) számíthatjuk ki: Marozsák Tóbiás (Budapest, Óbudai Árpád Gimn., 12. évf.) |