Feladat:	4956. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Berke Martin ,  Kolontári Péter ,  Póta Balázs
Füzet:	2018/február, 116 - 118. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Egyéb kényszermozgás
Hivatkozás(ok):	Feladatok: 2017/szeptember: 4956. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A súrlódásmentesen lecsúszó test sebességét a parabolatükör legmélyebb pontjában az energiamegmaradás törvényéből számíthatjuk ki: $\begin{array}{c}{\displaystyle mgH=\frac{1}{2}m{v}^2\mathrm{,}\text{ahonnan}v=\sqrt[]{2gH}\mathrm{.}}\end{array}$ A pálya legalsó pontjának közelében a test mozgása egyenletes körmozgással közelíthető. A körpálya sugara (a parabola simulókörének $R$ sugara) megegyezik a parabola $p$ paraméterével, ami a fókusztávolság kétszerese (lásd pl. https://hu.wikipedia.org/wiki/Fókusztávolság): $\begin{array}{c}{\displaystyle R=p=2f\mathrm{.}}\end{array}$ (Ugyanezt az összefüggést a gömbtükör fókusztávolságának ismert képlete alapján is megkaphatjuk.) A körmozgás dinamikai feltétele (az 1. ábra jelöléseit használva): $\begin{array}{c}{\displaystyle N-mg=m\frac{v^2}{R}\mathrm{,}}\end{array}$ ahonnan a keresett nyomóerő: 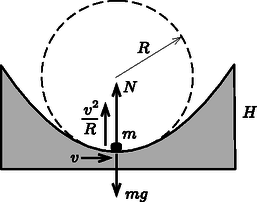$\begin{array}{c}{\displaystyle N=mg+m\frac{v^2}{2f}=mg+m\frac{2gH}{2f}=mg\left(1+\frac{H}{f}\right)\mathrm{.}}\end{array}$   1. ábra      Kolontári Péter (Pécs, Leővey Klára Gimn., 12. évf.)     II. megoldás. Vizsgáljuk meg, hogy hány metszéspontja lehet egy $f$ fókusztávolságú parabolának és a parabolát a talppontjánál érintő $r$ sugarú körnek! A görbék egyenlete $\begin{array}{c}{\displaystyle 4fy=x^2\mathrm{,}\text{illetve}{x}^2+{\left(y-r\right)}^2=r^2\mathrm{,}}\end{array}$ ahonnan a metszéspont(ok) $y$ koordinátáját megadó összefüggés: $\begin{array}{c}{\displaystyle y^2=2y\left(r-2f\right)\mathrm{.}}\end{array}$ Innen látható, hogy ($y\ge 0$ miatt) a két görbének csak akkor lesz egynél több metszéspontja, ha $r-2f>0$ (2. ábra). A legnagyobb kör, amelynek csak egyetlen közös pontja van a parabolával (ez felel meg a simulókörnek) $R=2f$ sug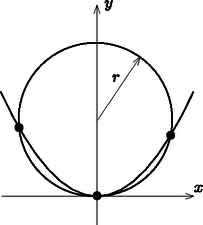arú.   2. ábra   Az energiamegmaradás alapján a test sebessége a pályájának legalsó pontjában $v=\sqrt[]{2gH}$. Newton II. törvénye szerint $\begin{array}{c}{\displaystyle N-mg=m\frac{2gH}{2f}\mathrm{,}}\end{array}$ innen a nyomóerő $\begin{array}{c}{\displaystyle N=mg\frac{H+f}{f}\mathrm{.}}\end{array}$    Póta Balázs (Győr, Révai M. Gimn., 11. évf.)     III. megoldás. A parabola talppontjának közvetlen közelében a test vízszintes irányú sebességét állandónak, $v=\sqrt[]{2gH}$ nagyságúnak tekinthetjük, a vízszintes irányú elmozdulást tehát minden pillanatban az $\begin{array}{c}{\displaystyle x\left(t\right)=vt=t\sqrt[]{2gH}}\end{array}$ összefüggésből számíthatjuk ki. Másrészt tudjuk, hogy a tükör forgásfelületének vezérgörbéje egy olyan parabola, amelynek egyenlete: $\begin{array}{c}{\displaystyle y=\frac{x^2}{4f}\mathrm{.}}\end{array}$ Ebből a két egyenletből megkapjuk (közelítőleg) a test függőleges irányú elmozdulását az idő függvényében: $\begin{array}{c}{\displaystyle y\left(t\right)=\frac{x{\left(t\right)}^2}{4f}=\frac{1}{2}\left(\frac{H}{f}g\right)t^2\equiv \frac{a}{2}{t}^2\mathrm{.}}\end{array}$ Látjuk, hogy a kis test $a=Hg/f$ nagyságú, függőlegesen felfelé irányuló gyorsulással mozog. Ilyen mozgást az $\begin{array}{c}{\displaystyle N-mg=ma}\end{array}$ mozgásegyenlet szerint $\begin{array}{c}{\displaystyle N=mg+ma=mg\left(1+\frac{H}{f}\right)}\end{array}$ erő képes létrehozni, tehát ekkora erővel nyomja a tükör a kis testet, és ugyanekkorával nyomja az is a tükröt.    Berke Martin (Zalaegerszegi Zrínyi M. Gimn., 12. évf.)  dolgozata alapján