Feladat:	4904. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Elek Péter ,  Fehér Szilveszter ,  Fekete Balázs Attila ,  Jakus Balázs István ,  Marozsák Tóbiás ,  Nagy Botond ,  Németh Róbert ,  Olosz Adél ,  Sal Dávid ,  Sz. K. ,  Szentivánszki Soma
Füzet:	2017/november, 500 - 502. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Egyéb áramkörök
Hivatkozás(ok):	Feladatok: 2017/január: 4904. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. A feltöltött ($C$ kapacitású és $Q_0=2C{U}_0$ töltésű) kondenzátor kezdeti polaritásától függően két eset lehetséges. I. eset: A kondenzátor pozitív töltésű fegyverzete a bal oldalon van (1. ábra). 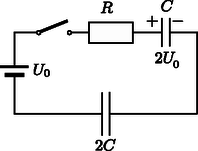  1. ábra   II. eset: A pozitív fegyverzet a jobb oldalra kerül (2. ábra). 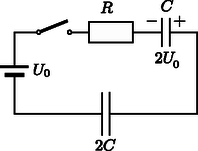  2. ábra   Vizsgáljuk először az első esetet. A kapcsoló zárása után az áramkörben töltésáramlás indul meg, melynek során mindkét kondenzátor töltött állapotba kerül (3. ábra). A folyamat végén a körben már nem folyik áram, ennek következtében az ellenálláson nem esik feszültség. Írjuk fel a huroktörvényt erre az állapotra a 3. ábra jelöléseit használva (az óramutató járásával azonos irányban): 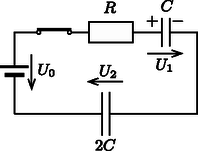$\begin{array}{c}{\displaystyle U_1+U_2-U_0=0.}\end{array}$ (1) Tudjuk továbbá, hogy a két kondenzátort összekötő ágon az összes töltés a kezdeti és végállapotban egyenlő (hiszen a kondenzátor lemezei között nem haladhatnak át töltések): $\begin{array}{c}{\displaystyle -2C{U}_0=-C{U}_1+2C{U}_2\mathrm{,}}\end{array}$ (2) innen $\begin{array}{c}{\displaystyle 2U_0=U_1-2U_2\mathrm{.}}\end{array}$ (3) Az (1) és (3) egyenletek rendszerének megoldása: $\begin{array}{c}{\displaystyle U_1=\frac{4}{3}{U}_0\mathrm{,}{U}_2=-\frac{1}{3}{U}_0\mathrm{.}}\end{array}$ A negatív előjel azt fejezi ki, hogy a $2C$ kapacitású kondenzátoron a lemezek töltése a 3. ábrán jelölthöz képest ellentétes (a bal oldali lemez lesz pozitív töltésű).   3. ábra   Jóllehet az ellenálláson áthaladó áram időben bonyolult módon (belátható, hogy exponenciális függvény szerint) változik, az ellenálláson fejlődő Joule-hő elemi úton (integrálszámítás nélkül) is kiszámítható, ha energetikai megfontolásokat követünk. Feltételezzük, hogy az áramkörből nem jut ki energia (elhanyagolva az áramok által keltett mágneses tér gerjesztette elektromágneses hullámokat), így teljesül a $\begin{array}{c}{\displaystyle W_{\text{telep}}+W_C+W_{2C}+W_R=0}\end{array}$ (4) mérlegegyenlet. A fenti képletben $W_{\text{telep}}$ a telep energiaváltozását, $W_C$ és $W_{2C}$ az egyes kondenzátorok energiaváltozását, $W_R$ pedig az ellenálláson fejlődő hőt jelöli. A kondenzátorok energiaváltozása: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle W_C}& {\displaystyle =\frac{1}{2}C\left(U_1^2-{\left(2U_0\right)}^2\right)=-\frac{10}{9}C{U}_0^2\mathrm{,}}\hfill \\ \hfill {\displaystyle W_{2C}}& {\displaystyle =\frac{1}{2}2C\left(U_2^2-0\right)=\frac{1}{9}C{U}_0^2\mathrm{,}}\hfill \end{array}}$ a telep energiaváltozása pedig az $U_0$ feszültség és a telepen áthaladó töltés szorzata: $\begin{array}{c}{\displaystyle W_{\text{telep}}=U_0\left(Q_0-C{U}_1\right)=U_0\left(2C{U}_0-C\cdot \frac{4}{3}{U}_0\right)=\frac{2}{3}C{U}_0^2\mathrm{.}}\end{array}$ (A pozitív előjel azt jelenti, hogy a telepnek nő az energiája.) A (4) energiamérleg segítségével kiszámíthatjuk az ellenálláson fejlődő hőt: $\begin{array}{c}{\displaystyle W_R=-W_{\text{telep}}-W_C-W_{2C}=-\frac{2}{3}C{U}_0^2-\left(-\frac{10}{9}C{U}_0^2\right)-\frac{1}{9}C{U}_0^2=\frac{1}{3}C{U}_0^2\mathrm{.}}\end{array}$ A második esetben a fentiekhez teljesen hasonló módon járhatunk el. A megfelelő egyenletek csak a $C$ kapacitású kondenzátor kezdeti töltését megadó kifejezés előjelében térnek el az első eset egyenleteitől: Az $\left(1\text{'}\right)$ $-$ $\left(3\text{'}\right)$ egyenletek megoldása: $\begin{array}{c}{\displaystyle U_1=\mathrm{0,}{U}_2=U_0\mathrm{.}}\end{array}$ (Ez azt jelenti, hogy a kapcsoló zárása után a $C$ kapacitású kondenzátor összes töltése átkerül a másik kondenzátorra.) Az energiaváltozások: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle W_C}& {\displaystyle =\frac{1}{2}C\left(0-{\left(2U_0\right)}^2\right)=-2C{U}_0^2\mathrm{,}}\hfill \\ \hfill {\displaystyle W_{2C}}& {\displaystyle =\frac{1}{2}2C\left(U_0^2-0\right)=C{U}_0^2\mathrm{,}}\hfill \\ \hfill {\displaystyle W_{\text{telep}}}& {\displaystyle =-U_0\cdot 2C{U}_0=-2C{U}_0^2\mathrm{.}}\hfill \end{array}}$ (A telep energiaváltozása ebben az esetben negatív, hiszen az áram a telepfeszültséggel ellentétes irányban folyik.) Az energiamérlegből: $\begin{array}{c}{\displaystyle W_R=-W_{\text{telep}}-W_C-W_{2C}=2C{U}_0^2-\left(-2C{U}_0^2\right)-C{U}_0^2=3C{U}_0^2\mathrm{.}}\end{array}$ Az ellenálláson fejlődő hő tehát a már kezdetben is feltöltött kondenzátor bekötésétől (polaritásától) függően $\frac{1}{3}C{U}_0^2$ vagy $3C{U}_0^2$.   Megjegyzés. Belátható, hogy ha egy ellenálláson időben exponenciálisan csökkenő áram folyik keresztül (esetünkben éppen ez történik), akkor a teljes kisülési folyamat során fejlődő Joule-hő az ellenállásra eső kezdeti (maximális) feszültség és az ellenálláson átfolyó töltés szorzatának felével egyezik meg. Valóban, ha az áramerősség $\begin{array}{c}{\displaystyle I\left(t\right)=I_0{\text{e}}^{-\lambda t}\mathrm{,}}\end{array}$ az ellenállásra eső feszültség tehát $\begin{array}{c}{\displaystyle U\left(t\right)=RI\left(t\right)=R{I}_0{\text{e}}^{-\lambda t}\mathrm{,}}\end{array}$ akkor a folyamat során fejlődő Joule-hő (ami az időben változó $P\left(t\right)=U\left(t\right)I\left(t\right)$ teljesítmény integrálja): $\begin{array}{c}{\displaystyle W_R=\underset{0}{\overset{\infty }{\int }}U\left(t\right)I\left(t\right)\text{d}t=R{I}_0^2\underset{0}{\overset{\infty }{\int }}{\text{e}}^{-2\lambda t}\text{d}t=\frac{R{I}_0^2}{2\lambda }\mathrm{.}}\end{array}$ Másrészt a kezdeti (maximális) feszültség az ellenálláson $\begin{array}{c}{\displaystyle U_{\text{max}}=U\left(0\right)=RI\left(0\right)=R{I}_0\mathrm{,}}\end{array}$ a rajta átfolyó töltés pedig $\begin{array}{c}{\displaystyle Q=\underset{0}{\overset{\infty }{\int }}I\left(t\right)\text{d}t=I_0\underset{0}{\overset{\infty }{\int }}{\text{e}}^{-\lambda t}\text{d}t=\frac{I_0}{\lambda }\mathrm{.}}\end{array}$ Látható, hogy a hivatkozott $W_R=\frac{1}{2}{U}_{\text{max}}Q$ összefüggés teljesül. A feladatban szereplő kapcsolásnál a keresett hő $\begin{array}{c}{\displaystyle \frac{1}{2}\left(-U_0\right)\left(-\frac{2}{3}C{U}_0\right)=\frac{1}{3}C{U}_0^2\mathrm{,}\text{illetve}\frac{1}{2}\left(3U_0\right)\left(2C{U}_0\right)=3C{U}_0^2\mathrm{.}}\end{array}$