Feladat:	2017. évi Nemzetközi Matematika Diákolimpia 13. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Kovács Benedek
Füzet:	2017/október, 389 - 391. oldal		PDF  |  MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia, Ellenpélda, mint megoldási módszer a matematikában, Teljes indukció módszere
Hivatkozás(ok):	Feladatok: 2017/szeptember: 2017. évi Nemzetközi Matematika Diákolimpia 13. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Kovács Benedek megoldása. A feladat állítása nem igaz: belátjuk, hogy a vadász akármilyen stratégiája esetén a nyomkövető jelezheti $P_1\mathrm{,}{P}_2\mathrm{,}\text{...}\mathrm{,}{P}_{{10}^9}$ pontok olyan sorozatát, hogy a nyúlnak létezzen olyan, a szabályok szerinti $A_0{A}_1{A}_2\text{...}{A}_{{10}^9}$ lehetséges mozgássorozata, amire $B_{{10}^9}{A}_{{10}^9}>100$. Vagyis ha a nyúl maga jelölheti ki a nyomkövető jelzéseit a számára legkedvezőbb módon, akkor a vadász nem tudja garantálni, hogy $100$-on belül kerüljön a nyúlhoz. Legyen $d_i=A_i{B}_i$. A nyúl célja az, hogy $d_{{10}^9}>100$ legyen. Nyilván az is elég számára, ha valamilyen $i<{10}^9$-re $d_i>100$, hiszen ha ekkor a nyúl a további lépésekben már mindig a vadásszal ellentétes irányban lép, akkor lépésével a vadásztól való távolságát 1-gyel növeli, a vadász pedig a saját lépésében legfeljebb 1-gyel csökkentheti, vagyis egy fordulón belül a távolság nem csökken, így a ${10}^9$-edik forduló után is 100-nál nagyobb lesz.   Lemma. Ha az $i$. fordulóban $d_i<100$, a vadász nem tudja garantálni, hogy $d_{i+200}^2\le d_i^2+\frac{1}{2}$ legyen.   Bizonyítás. A nyúl tehát 200 forduló alatt szeretné a vadásztól vett távolságának négyzetét $\frac{1}{2}$-nél többel megnövelni. A vadásznak az $i$-edik forduló kezdetekor a nyúl mozgásáról rendelkezésére álló információt a $P_1\mathrm{,}{P}_2\mathrm{,}\text{...}\mathrm{,}{P}_{i-1}$ pontok jelentik. Ezen pontok alapján a nyúlnak akár több lehetséges helye is lehet, de most tegyük fel még azt is, hogy a nyúl konkrétan elárulja a helyzetét, az $A_i$ pontot. A korábbi információk így feleslegessé válnak. Jelöljük $\ell$-lel az $A_i{B}_i$ egyenest ($A_i=B_i$ esetén tetszőleges egyenest $A_i$-n keresztül). Mérjük fel az ábra szerint az $l$ egyenesre az $A_i$ pontból, $B_i$-vel ellentétes irányban $\sqrt[]{39999}$ egységet, így kapva a $Z$ pontot. A $Z$ pontban merőlegest állítva $\ell$-re, ezen a merőlegesen vegyük fel a $C_1$ és $C_2$ pontokat $Z$-től 1 távolságra. Ekkor a Pitagorasz-tétel miatt $A_i{C}_1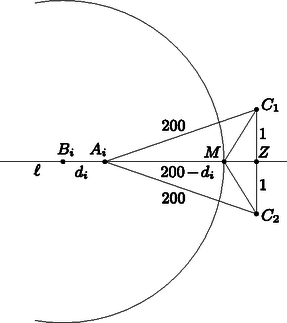=A_i{C}_2=\sqrt[]{39999+1}=200$ lesz.     A nyúl számára a következő 200 fordulóban az lesz a stratégia, hogy egyenesen elmegy a $C_1$ célpontba (ezt megteheti, hiszen $A_i{C}_1=200$). Mivel a teljes $A_i{C}_1$ szakasz 1 távolságon belül van az $\ell$ egyenestől, a nyúl minden fordulóban kijelölheti helyzetének az $\ell$-re vett merőleges vetületét, mint a nyomkövető által adandó jelzést. Természetesen ugyanezeket a jelzéseket megadhatná a nyúl akkor is, ha nem a $C_1$, hanem a $C_2$ pontba menne el hasonló módon, hiszen a két útvonal $\ell$-re nézve szimmetrikus. A vadász így a 200 forduló alatt kapott jelzésekből nem fogja tudni, hogy a $C_1$ vagy a $C_2$ pont felé tart-e a nyúl. Nézzük azt a $B_{i+200}$ pontot, ahova a vadász ezalatt eljutott. Ez a pont biztosan a $B_i$ középpontú, 200 sugarú körön belül van, legyen ennek az $\ell$-lel való (a nyúl irányába eső) metszéspontja $M$. Osszuk fel ezt a kört két részre az $\ell$ egyenes ($C_1{C}_2$ felezőmerőlegese) mentén. Az egyik (az ábra szerint felső) részben lévő pontok a $C_1$ célponthoz, a másik (alsó) részben lévők $C_2$-höz vannak közelebb. A felső rész összes pontjára igaz, hogy legalább olyan távol vannak $C_2$-től, mint $M$, mert mind vízszintesen, mind függőlegesen legalább olyan távol vannak tőle (ha az ábra szerint, vagyis az $\ell$ egyenessel párhuzamosnak vesszük a vízszintes irányt). Ugyanígy az alsó rész összes pontja legalább olyan távol van $C_1$-től, mint $M$. Így a két lehetséges célpont közül a távolabbi mindenképpen legalább olyan messze lesz a vadásztól, mint az $M{C}_1=M{C}_2$ távolság. Számítsuk ki ezt a távolságot. $B_i{A}_i=d_i$, így $A_{i}M=200-d_i$. Így $MZ=A_{i}Z-A_{i}M=\sqrt[]{39999}-200+d_i$, és a Pitagorasz-tétel alapján $\begin{array}{c}{\displaystyle M{C}_1=\sqrt[]{M{Z}^2+C_1{Z}^2}=\sqrt[]{{\left(\sqrt[]{39999}-200+d_i\right)}^2+1}\mathrm{.}}\end{array}$ Azt kell belátnunk, hogy ez a távolság nagyobb, mint $\sqrt[]{d_i^2+\frac{1}{2}}$: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \sqrt[]{{\left(\sqrt[]{39999}-200+d_i\right)}^2+1}}& {\displaystyle >\sqrt[]{d_i^2+\frac{1}{2}}\mathrm{,}}\hfill \\ \hfill {\displaystyle {\left(\sqrt[]{39999}-200+d_i\right)}^2+1}& {\displaystyle >d_i^2+\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle d_i^2+2\left(\sqrt[]{39999}-200\right)d_i+80000-400\sqrt[]{39999}}& {\displaystyle >d_i^2+\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle 2\left(\sqrt[]{39999}-200\right)d_i-400\sqrt[]{39999}+80000}& {\displaystyle >\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle 2\left(\sqrt[]{39999}-200\right)d_i+400\left(200-\sqrt[]{39999}\right)}& {\displaystyle >\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle \left(400-2d_i\right)\left(200-\sqrt[]{39999}\right)}& {\displaystyle >\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle \left(200-d_i\right)\left(200-\sqrt[]{39999}\right)}& {\displaystyle >\frac{1}{4}\mathrm{.}}\hfill \end{array}}$ Mivel $d_i\le 100$, azaz $200-d_i\ge 100$, elég belátni, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 200-\sqrt[]{39999}}& {\displaystyle >\frac{1}{400}\mathrm{,}}\hfill \\ \hfill {\displaystyle 80000-400\sqrt[]{39999}}& {\displaystyle >\mathrm{1,}}\hfill \\ \hfill {\displaystyle 79999}& {\displaystyle >400\sqrt[]{39999}\mathrm{.}}\hfill \end{array}}$ Négyzetre emelve: $\begin{array}{c}{\displaystyle 79{999}^2>39999\cdot {400}^2\mathrm{.}}\end{array}$ Ez pedig igaz, mert $\begin{array}{c}{\displaystyle 79{999}^2-1=80000\cdot 79998=160000\cdot 39999=39999\cdot {400}^2\mathrm{.}}\end{array}$ Ekvivalens lépésekkel dolgoztunk, így a vadász számára rosszabbik távolság legalább $M{C}_1>\sqrt[]{d_i^2+\frac{1}{2}}$, így a lemmát beláttuk.   A lemmából már következik a bizonyítandó állítás: a játék elején $d_0^2=0$, és a lemma szerint (teljes indukcióval) a vadász számára legrosszabb esetben $d_{200n}^2>\frac{1}{2}n$, amíg a távolság el nem éri a $100$-at. Ez az elérés pedig legkésőbb $n=2\cdot {100}^2=20000$-re bekövetkezik, azaz $200\cdot 20000=4\cdot {10}^6$ fordulón belül. Vagyis $d_{4\cdot {10}^6}^2>10000$, azaz $d_{4\cdot {10}^6}>100$. A nyúl ezzel elérte a célját, hiszen $4\cdot {10}^6\le {10}^9$.