Kezdőlap


Feladat:	4910. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kondákor Márk , Németh Róbert , Szakály Marcell
Füzet:	2017/október, 433 - 436. oldal		PDF \| MathML
Témakör(ök):	Feladat, Egyenletes mozgás (Egyenes vonalú mozgások), Fermat-elv
Hivatkozás(ok):	Feladatok: 2017/február: 4910. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat többféle módszerrel is megoldható. Az alább bemutatott eljárások közül kettő fizikai (optikai, illetve hangtani) megfontolásokra épül, a harmadik a differenciálszámítás matematikai apparátusának felhasználásával jut el a végeredményig. (A három különböző gondolatmenetű megoldás jelöléseit úgy változtattuk meg, hogy az eredmények egymással könnyen összehasonlíthatóak legyenek. ‐ A Szerk.)

I. megoldás. Oldjuk meg a feladatot fizikai eszközökkel! Használjuk a fényterjedést leíró Fermat-elvet: a fény két pont között olyan útvonalon terjed, amely mentén a fényterjedés ideje a szomszédos (a tényleges útvonaltól csak kicsit eltérő) útvonalak idejéhez képest a lehető legkisebb.
Tegyük fel, hogy az ösvény

B

-vel átellenes felén mindenhol

k u

sebességgel haladhatunk, és az

A

pont az ösvénytől egy ,,hajszálnyi'' távolságra, de már az ösvény túloldalán helyezkedik el. (Ez érdemben nem módosítja a feladatot, hiszen ha már egyszer elértük az ösvényt, azon nyilván gyorsan és egyenesen érdemes haladjunk, nem pedig a túloldali erdőben görbe útvonal mentén és lassabban.)
Ebben az új megfogalmazásban a probléma a következő kérdéssel egyenértékű: Miként juthat el a fény egy optikailag sűrűbb közeg

B

pontjából az optikailag ritkább közeg

A

pontjába, ha a két közeget egy sík felület választja el egymástól és a relatív törésmutató (a fénysebességek aránya)

k

?
A

B

pontból kiinduló fénysugarak a két közeg határán megtörnek, illetve visszaverődnek. Ha a

k

törésmutató ,,elegendően nagy'', akkor a törési törvény szerint lesz egy olyan fénysugár, amelynek törési szöge

90^{\circ}

, vagyis amelyik fénysugár a két közeg határán (az ösvény mentén) halad tovább és jut el az

A

pontig (1a. ábra). Ezen fénysugár beesési szöge az ábra jelöléseit használva éppen

90^{\circ} - φ

, így a Snellius‐Descartes-törvény szerint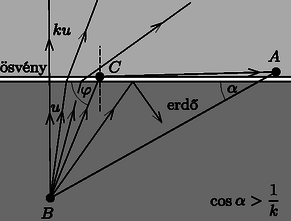

\begin{matrix} \frac{sin (90^{\circ} - φ)}{sin 90^{\circ}} = cos φ = \frac{1}{k} . \end{matrix}

A közeghatárt a

C

ponttól balra elérő fénysugarak átjutnak az optikailag ritkább közegbe, a

C

-től jobbra érkező fénysugarak pedig teljes visszaverődést szenvednek. Az ábrán látható

φ

szög nyilván nagyobb, mint

α

, tehát a megadott

k

és

α

adatok között fenn kell álljon a

cos α > \frac{1}{k}

egyenlőtlenség; ez adja meg az ,,elegendően nagy törésmutató'' kifejezés pontos jelentését.

1a. ábra

Amennyiben a törésmutató nem túl nagy (vagyis

cos α < 1 / k

), a

B

-ből kiinduló fénysugarak egyike törésmentesen, mindvégig az optikailag sűrűbb közegben haladva jut el az

A

pontig (1b. ábra). Ilyen körülmények között az eredeti feladat megoldása: érdemes mindvégig az erdőben maradnunk, és ott egyenes úton haladva juthatunk el leghamarabb a

B

pontból az

A

ponti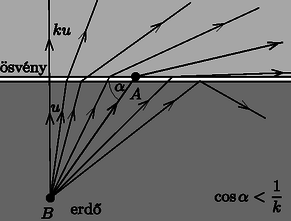g.

1b. ábra

II. megoldás. Ha a

B

pontból valamilyen úton haladva a legrövidebb idő alatt jutunk az

A

pontba, akkor nyilván ugyanezen az útvonalon juthatunk leghamarabb az

A

pontból a

B

pontba. Vizsgáljuk a továbbiakban ezt a ,,megfordított'' problémát!
Képzeljük el, hogy az

A

pontból indulva egy hangforrás mozog az ösvény mentén

k u

sebességgel, miközben folyamatosan olyan hanghullámokat kelt, amelyek

u

sebességgel terjednek az erdőben

(k > 1)

. Hol helyezkednek el azok a pontok, amelyeket a hanghullámok elérnek a hullámforrás indulásától számított

t

idő alatt? A különböző helyekről különböző időpillanatokban kiinduló gömbhullámok egy kúpot (az ún. Mach-kúpot) jelölnek ki (2a. ábra). A kúp csúcsa

k u

sebességgel mozog, a kúp félnyílásszöge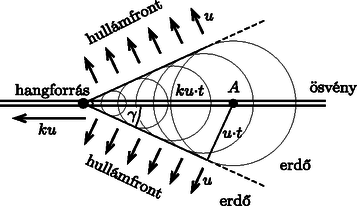

\begin{matrix} γ = arcsin \frac{u}{k u} = arcsin \frac{1}{k}, \end{matrix}

a kúp alkotói pedig

u

sebességgel mozogva távolodnak a szimmetriatengelytől (vagyis az ösvénytől). A

γ

szög (az ún. Mach-szög) egyértelműen meghatározható, hiszen a feladat szövege szerint

k > 1

2a. ábra

Az idő múltával lesz egy olyan pillanat, amikor az egyre táguló kúp alkotója (vagyis a hullámfront) eléri a

B

pontot (2b. ábra). Tekintsük a

B

ponton átmenő, a hullámfrontra merőleges egyenes és az ösvény metszéspontját. Ezen

C

pontból kiinduló hullám éri el leghamarabb a

B

pontot, tehát ezen a ponton vezet át az eredeti feladat megoldása, a legrövidebb idejű útvonal is. Ezek szerint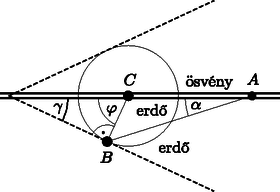

\begin{matrix} φ = 90^{\circ} - γ, vagyis cos φ = sin γ = \frac{1}{k} . \end{matrix}

2b. ábra

Természetesen (az ábrán választott mozgásirány esetén) a

C

pont nem lehet

A

-tól jobbra, vagyis

φ \geq α

. Emiatt a fentebb leírt megoldás csak

\begin{matrix} cos α \geq cos φ = \frac{1}{k} \end{matrix}

teljesülése esetén helyes. A

k cos α = 1

határesetben

φ = α

, vagyis a

C

pont egybeesik

A

-val. Ilyenkor a legrövidebb idő, ami alatt eljuthatunk

A

-ból

B

-be (vagy

B

-ből

A

-ba) olyan útnak felel meg, amely mindvégig az erdőben halad.
Vajon melyik útvonalon haladó hullám éri el leghamarabb a

B

pontot, ha

k cos α < 1

? Ebben az esetben nem a Mach-kúp hullámfrontja, hanem az

A

pontból kiinduló gömbhullám éri el elsőként a

B

pontot (2c. ábra), vagyis a legrövidebb idejű mozgás mindvégig az erdőben halad.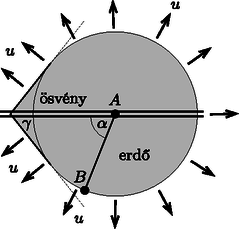

2c. ábra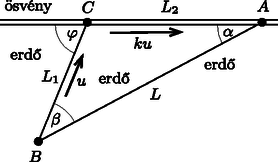

III. megoldás. Jelöljük az

A

és

B

pont távolságát

L

-lel, azt a pontot pedig, ahol elérjük az ösvényt,

C

-vel (3. ábra). Az

A

és

C

, valamint a

C

és

B

pontok között nyilván egyenes utat érdemes választanunk. Az erdőben megtett út irányát a

B A

iránytól mért

β

szöggel, vagy az ösvény irányához viszonyított

φ = α + β

szöggel jellemezhetjük.

3. ábra

Az erdőben megtett út hossza (a szinusztétel alapján)

L_{1} = \frac{sin α}{sin (α + β)} L

, az ösvényen megtett út hossza pedig

L_{2} = \frac{sin β}{sin (α + β)} L

. A teljes menetidő a

β

szög függvényében:

\begin{matrix} t (β) = \frac{L_{1}}{u} + \frac{L_{2}}{k u} \equiv \frac{L}{u} \cdot \frac{sin α + \frac{1}{k} sin β}{sin (α + β)} . \end{matrix}

A függvény (számunkra érdekes) értelmezési tartománya

0 \leq β \leq 90^{\circ} - α

, hiszen nyilván nem éri meg az ösvényt (az ábrán vázolt elrendezés esetén) az

A

ponttól jobbra, vagy a

B

-hez legközelebbi ponttól balra elérni.
A menetidő minimumát a

t (β)

függvény deriváltjának eltűnése határozhatja meg. Ha létezik olyan

β

szög az értelmezési tartomány belsejében, ahol

\begin{matrix} 0 & = t' (β) = \frac{L}{u} \cdot \frac{\frac{1}{k} cos β sin (α + β) - cos (α + β) (sin α + \frac{1}{k} sin β)}{sin^{2} (α + β)} = \\ = \frac{L}{u} \cdot \frac{sin α}{sin^{2} (α + β)} [\frac{1}{k} - cos (α + β)], \end{matrix}

ott a haladási időnek szélsőértéke (esetünkben minimuma) lehet. Mivel sem

(L / u) sin α

, sem pedig

sin (α + β) \equiv sin φ

nem lehet nulla, a derivált csak akkor válhat nullává, ha

\begin{matrix} \frac{1}{k} = cos (α + β), vagyis k cos φ = 1. \end{matrix}

Mivel

β \geq 0

, vagyis

φ \geq α

, a derivált nullává válásának feltétele csak

\begin{matrix} 1 = k cos φ \leq k cos α \end{matrix}

esetben teljesülhet.
Amennyiben

k cos α < 1

áll fenn, a

t (β)

függvény monoton növekszik, így a legrövidebb idő a

β = 0

szöghöz tartozik. Ilyen esetben (vagyis amikor az ösvényen haladás sebessége nem ,,elég nagy'') érdemes mindvégig az erdőben haladjunk, egyenes vonalban

B

-től az

A

pontig.