Feladat:	B.4791	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Andó Angelika ,  Cseh Kristóf ,  Csorba Benjámin ,  Fuisz Gábor ,  Horváth András János ,  Kocsis Júlia ,  Kondákor Márk ,  Nagy Dávid Paszkál ,  Polgár Márton ,  Szabó Dávid ,  Vágó Ákos ,  Váli Benedek
Füzet:	2017/szeptember, 339 - 343. oldal		PDF  |  MathML
Témakör(ök):	Síkgeometriai bizonyítások, Feladat, Magasságvonal, Húrnégyszögek
Hivatkozás(ok):	Feladatok: 2016/április: B.4791

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Először tisztázzunk elfajuló, illetve lehetetlen eseteket. A $D$ vagy $E$ pontok akkor eshetnek egybe valamelyik csúccsal, ha a háromszög derékszögű. Ha a derékszög $B$-nél van, akkor $D\equiv E\equiv B$, nem jöhetett létre a $DE$-egyenes. Ha $A$-nál vagy $C$-nél van (mivel a két eset lényegében ugyanaz, elég pl. csak az $A$ csúcsra vizsgálni), akkor $A\equiv E\equiv M$, így $P\equiv M$, vagyis most a $PM$-egyenes nem jöhetett létre. Ezeken az eseteken kívül $M$ nem eshet egybe se talpponttal, se csúccsal, se $P$-vel. Lehetséges még, hogy $AC||DE$, ilyenkor $AEDC$ húrtrapéz, így $BAC\sphericalangle =BCA\sphericalangle$ miatt $ABC$ egyenlő szárú. Tehát fel kell tenni még, hogy $BC\ne AB$. Legyen az $AC$ szakasz felezőpontja $G$. Bizonyítandó, hogy $BG\perp PM$. Mivel $CDA\sphericalangle =CEA\sphericalangle ={90}^{\circ }$, azért $D$ és $E$ az $AC$ szakasz Thálesz-körére illeszkedik. Ezt a kört jelölje $k$. Másrészt $MDB\sphericalangle =BEM\sphericalangle ={90}^{\circ }$, ezért $D$ és $E$ a $BM$ szakasz Thálesz-körére is illeszkedik. Legyen ez a kör $\ell$, a középpontja pedig $BM$ felezőpontja, $H$. Most azt bizonyítjuk, hogy a $GD$ szakasz (és hasonló módon a $GE$ szakasz) az $\ell$ körhöz húzott érintőszakasz. $G$, $D$ és $H$ az $ABC$ háromszög Feuerbach-körére1 illeszkednek (melyet az 1. ábrán $f$-fel jelölünk), a körülírt kör $K$ középpontját viszonyítási pontnak választva pedig 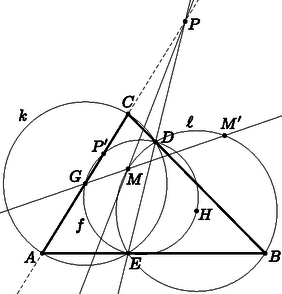${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{\overrightarrow{G}+\overrightarrow{H}}{2}}& {\displaystyle =\frac{\frac{\overrightarrow{A}+\overrightarrow{C}}{2}+\frac{\left(\overrightarrow{A}+\overrightarrow{B}+\overrightarrow{C}\right)+\overrightarrow{B}}{2}}{2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{\overrightarrow{A}+\overrightarrow{B}+\overrightarrow{C}}{2}\mathrm{,}}\hfill \end{array}}$ ami a Feuerbach-kör középpontjának helyvektora (felhasználtuk a $\begin{array}{c}{\displaystyle \overrightarrow{KM}=\overrightarrow{KA}+\overrightarrow{KB}+\overrightarrow{KC}}\end{array}$ összefüggést is). Így $GH$ átmérő, a Thálesz-tétel miatt $GDH\sphericalangle ={90}^{\circ }$, $GD$ csakugyan érintőszakasz.   1. ábra   Most invertáljunk $k$-ra. A $GD$ szakasz a $k$ kör sugara, ezért ‐ a szelőszorzat-tételt is figyelembe véve ‐ $\ell$-nek a $k$-ra invertált képe önmaga. Keressük $P$ képét. Az inverzió illeszkedéstartó, így $P$ egyrészt a $DE$ egyenes képére illeszkedik. A $D$ és az $E$ fixpontok, az egyenes pedig nem megy át $G$-n, így $DE$ képe egy $G$-n átmenő kör: $DEG$ körülírt köre, ami ismét $ABC$ Feuerbach-köre. Másrészt $P$ illeszkedik $AC$ képére, ami fixegyenes. Így $P\text{'}$ az $AC$ oldalegyenes és a Feuerbach-kör metszéspontja. Két ilyen pont van: az egyik $G$, de az $k$ középpontja, így nem lehet $P$ képe. A másik a $B$-hez tartozó magasság talppontja, így ez a magasságtalppont lesz $P$ képe. (Megjegyzés: ha a magasságtalppont és $G$ egybeesnek, akkor $ABC$ egyenlő szárú lett volna, amit kizártunk.) Így $GPB\sphericalangle ={90}^{\circ }$. (Ha $D$, $E$ és $G$ egy egyenesen lennének, akkor $DE$ is $k$ átmérője lenne, így a Thálesz-tétel szerint $ECD\sphericalangle =DAE\sphericalangle ={90}^{\circ }$ is igaz lenne, vagyis az $ABC$ háromszög $AE$ és $CD$ oldalegyenesei párhuzamosak lennének, ami lehetetlen.) Most határozzuk meg $M\text{'}$-t is. Ez rajta van az $\ell$ fixkörön, így $GM$ és $\ell$ második metszéspontja. Mivel az $\ell$ kör $BM$ Thálesz-köre, így $GM\text{'}B\sphericalangle =MM\text{'}B\sphericalangle ={90}^{\circ }$ (ha $M$ és $M\text{'}$ fordított sorrendben helyezkednek el, akkor is igaz az állítás, mert kiegészítő szögek lesznek). Most már meghatározhatjuk $PM$ képét. $G$-n nem mehet át, mert akkor az $M$ pont $PG\equiv AC$-n lenne, ami a derékszögű háromszög lehetetlen esetéhez vezet vissza. Így $PM$ képe a $G$-n, $P\text{'}$-n és $M\text{'}$-n átmenő kör. Mivel $GM\text{'}B\sphericalangle =GP\text{'}B\sphericalangle ={90}^{\circ }$, azért ez $BG$ Thálesz-köre. Eközben $BG$ egy $G$-n átmenő egyenes, így képe önmaga. Tehát $PM$ képének centrálisa a $BG$ egyenes, $BG$ képe. Ez kör és egyenes között derékszöget jelent, így mivel az inverzió szögtartó, az eredeti $PM$ egyenes és $BG$ is merőlegesek voltak. Ezt kellett bizonyítani. 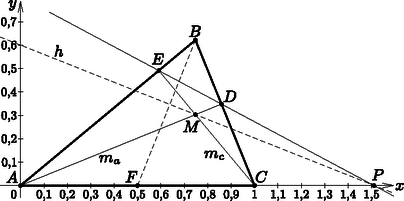  II. megoldás. Legyenek az $A$, $B$ illetve $C$ pont koordinátái rendre $\left(0;0\right)$, $\left(a;b\right)$, $\left(1;0\right)$, ahol $b\ne 0$, így állhat majd a számolás során törtek nevezőjében.   2. ábra   A továbbiakban két főbb dolgot fogunk használni: ‐ Adott $\left(x_1;y_1\right)$ és $\left(x_2;y_2\right)$ pontokon átmenő egyenes egyenlete: $\begin{array}{c}{\displaystyle y=\frac{y_1-y_2}{x_1-x_2}x+\left(y_1-\frac{y_1-y_2}{x_1-x_2}{x}_1\right)\mathrm{.}}\end{array}$ ‐ Két, a tengelyekkel nem párhuzamos egyenes akkor merőleges egymásra, ha meredekségeik szorzata $-1$. Az $AB$ egyenes egyenlete: $y=\frac{b}{a}x$. A $BC$ egyenes egyenlete: $y=-\frac{b}{1-a}x+\frac{b}{1-a}$. A $CE$ egyenes egyenlete: $y=-\frac{a}{b}x+\frac{a}{b}$ (az állandót onnan tudjuk, hogy az egyenes átmegy a $C$ ponton). Az $AD$ egyenlete: $y=\frac{1-a}{b}x$. Ha $a=0$ vagy $a=1$, akkor az $ABC$ háromszög $A$-ban vagy $C$-ben derékszögű, $D$ és $E$ egyike az $x$ tengelyen van, egybeesik $M$-mel és a derékszögű csúccsal, így $P$ is egybeesik $M$-mel, tehát $P$ és $M$ nem határoz meg egyenest. Ezeket az értékeket tehát kizárhatjuk. Tudjuk, hogy $D$ rajta van a $BC$ és $m_a$ egyeneseken, tehát felírható a következő egyenlet (a $D$ pont első koordinátája a következő egyenletben $x$): ${\displaystyle \begin{array}{c}\hfill {\displaystyle -\frac{b}{1-a}\cdot x+\frac{b}{1-a}-\frac{1-a}{b}\cdot x=\mathrm{0,}}\hfill \\ \hfill {\displaystyle x=\frac{b^2}{{\left(1-a\right)}^2+b^2}\mathrm{.}}\hfill \end{array}}$ (A számlálóban két nem 0 értékű szám négyzetének összege áll, tehát biztosan nem 0.) A $D$ pont második koordinátája: $\begin{array}{c}{\displaystyle \frac{1-a}{b}\cdot \frac{b^2}{{\left(1-a\right)}^2+b^2}=\frac{b\left(1-a\right)}{{\left(1-a\right)}^2+b^2}\mathrm{.}}\end{array}$ Tudjuk, hogy $E$ rajta van az $AB$ és $m_c$ egyeneseken, tehát felírható a következő egyenlet (az $E$ pont első koordinátája a következő egyenletben $x$): ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{b}{a}x-\left(-\frac{a}{b}x+\frac{a}{b}\right)=\mathrm{0,}}\hfill \\ \hfill {\displaystyle x=\frac{a^2}{a^2+b^2}\mathrm{.}}\hfill \end{array}}$ Itt $b\ne 0$, ezért a számláló sem 0. Az $E$ pont második koordinátája: $\begin{array}{c}{\displaystyle \frac{b}{a}\cdot \frac{a^2}{a^2+b^2}=\frac{ab}{a^2+b^2}\mathrm{.}}\end{array}$ A $DE$ egyenes meredeksége: $\begin{array}{c}{\displaystyle \frac{\frac{b\left(1-a\right)}{{\left(1-a\right)}^2+b^2}-\frac{ab}{a^2+b^2}}{\frac{b^2}{{\left(1-a\right)}^2+b^2}-\frac{a^2}{a^2+b^2}}\mathrm{.}}\end{array}$ A nevezőben a $D$ és az $E$ pont első koordinátájának különbsége áll. Ha ez 0, akkor a két pont egybeesik egymással és a $B$ csúccsal, vagyis az $ABC$ háromszög $B$-ben derékszögű. Ekkor a feladat nem értelmezhető, így feltesszük, hogy ez nem igaz. A kifejezést egyszerűsítve a következőt kapjuk: $\frac{\left(1-2a\right)b}{-a^2+a+b^2}$. (Lépések: $\left(a^2+b^2\right)$-tel, illetve $\left({\left(1-a\right)}^2+b^2\right)$-tel való bővítés, szorzattá alakítás, $b^2+a^2-1$ szorzótényezővel való egyszerűsítés. Ha ez utóbbinak 0 lenne az értéke, akkor a nevező is 0 lenne, viszont nem 0 értékről indultunk, és csak szoroztunk nem 0 értékű kifejezésekkel, tehát nem lehet 0 a nevező. A végeredmény így egy értelmezhető tört.) Mivel $1-2a=0$ esetén $AB=BC$, és ekkor nem jönne létre a $P$ metszéspont, ezért feltehetjük, hogy $1-2a\ne 0$. Mivel az egyenes átmegy az $E$ ponton, a képletében szereplő konstans értéke: $\begin{array}{c}{\displaystyle \frac{ab}{a^2+b^2}-\frac{\left(1-2a\right)b}{-a^2+a+b^2}\cdot \frac{a^2}{a^2+b^2}\mathrm{,}}\end{array}$ aminek egyszerűbb alakja $\frac{ab}{-a^2+a+b^2}$. (Lépések: $0\ne \left(-a^2+a+b^2\right)$-tel való bővítés, összevonás, szorzattá alakítás, $0\ne \left(a^2+b^2\right)$-tel való egyszerűsítés. Így a végeredmény egy értelmezhető tört.) A $DE$ egyenes egyenlete tehát: $\begin{array}{c}{\displaystyle y=\frac{\left(1-2a\right)b}{-a^2+a+b^2}x+\frac{ab}{-a^2+a+b^2}\mathrm{.}}\end{array}$ A $P$ pontról tudjuk, hogy rajta van az $AC$ egyenesen, vagyis második koordinátája 0, és rajta van a $DE$ egyenesen, tehát felírható a következő egyenlet a $P$ pont első koordinátájára: $\frac{\left(1-2a\right)bx+ab}{-a^2+a+b^2}=0$. Ez akkor igaz, ha $\left(1-2a\right)bx+ab=0$, vagyis $x=\frac{-a}{1-2a}$. Az $M$ pont első koordinátája $a$, ugyanis a $BM$ egyenes merőleges az $x$ tengelyre. Mivel $M$ rajta van az $m_a$ egyenesen, második koordinátája $\frac{1-a}{b}a=\frac{a-a^2}{b}$. A $PM$ egyenes meredeksége: $\begin{array}{c}{\displaystyle \frac{\frac{a-a^2}{b}-0}{a-\frac{-a}{1-2a}}=\frac{\frac{a-a^2}{b}}{\frac{2a-2a^2}{1-2a}}=\frac{\frac{1}{b}}{\frac{2}{1-2a}}=-\frac{1-2a}{2b}\mathrm{.}}\end{array}$ $F$ koordinátái $\left(0;\mathrm{0,5}\right)$, ugyanis $AC$ felezőpontja. Tehát a $BF$ egyenes egyenlete: $\frac{b-0}{a-\mathrm{0,5}}=\frac{2b}{2a-1}$. Mivel $-\frac{1}{\frac{2b}{2a-1}}=-\frac{1-2a}{2b}$, azért $BF$ merőleges $PM$-re.   Megjegyzések. 1. A fő hiba a megoldásokban a diszkusszió hiánya volt. Ez a koordinátageometriai megoldásokban nem csupán geometriai, de algebrai hiányt is jelent, jellemzően 0-val való osztást. 2. Többen a számos fellépő húrnégyszöget használták ki, támaszkodva a kerületi szögek tételére, illetve bizonyos esetekben a hatványvonal tulajdonságaira; mivel sok kört lehetett észrevenni, több különböző úton is el lehetett jutni a megoldáshoz. Egy ilyen megoldás olvasható honlapunkon: https://www.komal.hu/verseny/feladat.cgi?a=feladat&f=B4791&l=hu. 1https://hu.wikipedia.org/wiki/Feuerbach-kör.