Kezdőlap


Feladat:	B.4846	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Imolay András , Kerekes Anna , Zsigri Bálint
Füzet:	2017/május, 280 - 282. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Indirekt bizonyítási mód, Ponthalmazok
Hivatkozás(ok):	Feladatok: 2017/január: B.4846

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megjegyzés. A feladat szövegéből sajnálatosan kimaradt, hogy síkban vagy térben értendő, a beküldők nagyjából fele-fele arányban választották az egyik, illetve másik lehetőséget. Szerkesztőségi döntés alapján mindkét értelmezést teljes értékűnek fogadtuk el, mivel a térbeli esetet nem ítéljük lényegesen nehezebbnek a síkbelinél. Tekintsünk ugyanis egy $S$ síkot, amely az adott öt darab $S_{1}^{+}, ..., S_{5}^{+}$ félsík egyikére sem merőleges. Vetítsük le a félsíkokat merőlegesen az $S$ síkra. Az $S$ sík választása miatt a vetületek is félsíkok, jelölje őket rendre ${\hat{S}}_{1}^{+}, ..., {\hat{S}}_{5}^{+}$ . Ha valamely négy vetület metszete, mondjuk ${\hat{S}}_{1}^{+} \cap ... \cap {\hat{S}}_{4}^{+}$ korlátos, akkor őseik metszete, $S_{1}^{+} \cap ... \cap S_{4}^{+}$ is korlátos, ugyanis az $S_{1}^{+} \cap ... \cap S_{4}^{+}$ metszet illeszkedik pl. $S_{1}^{+}$ síkjára, amely nem merőleges $S$ -re. Így a síkbeli változatból azonnal következik, hogy az állítás térben is igaz. A közölt mintamegoldás a síkbeli esettel foglalkozik.

Megoldás. Jelölje a félsíkokat határoló egyeneseket

a

b

c

d

és

e

, a megfelelő félsíkokat pedig

a_{+}

b_{+}

c_{+}

d_{+}

és

e_{+}

.
Két félsíkot azonos állásúnak nevezünk, ha metszetük is egy félsík. Ez pontosan akkor történhet meg, ha határoló egyeneseik párhuzamosak, és a metszetük egybeesik valamely félsíkkal, rövidebben: ha az egyik félsík tartalmazza a másikat. Tegyük fel, hogy a félsíkokat meghatározó

a

b

c

d

és

e

egyenesek között van három párhuzamos. Az általuk meghatározott félsíkok között a skatulya-elv szerint van kettő azonos állású, ezek közül a bővebbet elhagyva a megmaradó négy metszete megegyezik az eredeti öt metszetével, vagyis korlátos. A továbbiakban feltesszük, hogy

a

b

c

d

és

e

közül mindegyik legfeljebb egy másikkal párhuzamos.
Válasszuk úgy a koordinátarendszert, hogy az

e

egyenes épp az

y

-tengelyre essen, az

e_{+}

félsík pedig az

x \geq 0

pontokból álljon. Az előbbiek szerint feltehető, hogy az

a

b

és

c

egyenesek nem párhuzamosak

e

-vel. Az

a_{+}

félsíkot nevezzük ,,fentinek'', ha pontosan azokból az

(x, y)

pontokból áll, amelyekre

y \geq y_{0}

, ahol

(x, y_{0})

a

egyenes pontja. Szemléletesen a definíció világos, az

a

egyenes feletti félsík

a_{+}

. Hasonlóan beszélhetünk lenti félsíkról, valamint értelemszerűen

b_{+}

és

c_{+}

félsíkok is fentiek vagy lentiek. (Ha a határoló egyenes párhuzamos az

y

-tengellyel, a definíció nem értelmes, de ezt az esetet kizártuk.)
Ismét a skatulya-elv szerint

a_{+}

b_{+}

és

c_{+}

között van kettő, ami egyszerre fenti, vagy lenti. Feltehető tehát, hogy

a_{+}

és

b_{+}

is fenti. (Ha mindkettő lenti, tükrözzünk az

x

-tengelyre.) Ha az

a

és

b

egyenesek párhuzamosak, akkor

a_{+}

és

b_{+}

azonos állásúak, közülük a bővebbet elhagyva a megmaradó négy metszete megegyezik az eredeti öt metszetével, vagyis korlátos. Legyen tehát

a

és

b

metszéspontja

C (c_{x}, c_{y})

, az

y

-tengelyt pedig messék az

A (0, a_{y})

, illetve

B (0, b_{y})

pontokban. Szintén az általánosság megszorítása nélkül feltehető, hogy

a_{y} \geq b_{y}

. Ha

c_{x} \leq 0

, akkor

a_{+} \cap e_{+}

metszetet tartalmazza

b_{+}

, ezért

b_{+}

-t elhagyva az öt félsíkból a metszet nem változik, így korlátos marad. Ha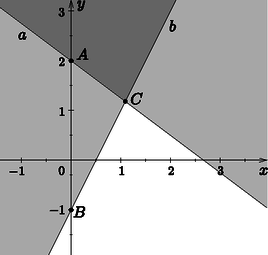

c_{x} > 0

, akkor

e_{+} \cap b_{+} = (e_{+} \cap a_{+} \cap b_{+}) \cup A B C ▵

. Ezért

\begin{matrix} b_{+} \cap c_{+} \cap d_{+} \cap e_{+} = c_{+} \cap d_{+} \cap (e_{+} \cap b_{+}) = \\ = & c_{+} \cap d_{+} \cap ((e_{+} \cap a_{+} \cap b_{+}) \cup A B C ▵) = \\ = & (a_{+} \cap b_{+} \cap c_{+} \cap d_{+} \cap e_{+}) \cup (c_{+} \cap d_{+} \cap A B C ▵), \end{matrix}

ahol az első tag a feltevés szerint korlátos, a második pedig az

A B C ▵

része, így szintén korlátos. A két korlátos halmaz uniója is korlátos, amivel az állítást beláttuk.

Megjegyzés. A legtöbb megoldó az öt félsík lehetséges metszete szerinti esetvizsgálatot végzett. Tipikus hiba volt, hogy a megoldó nem foglalkozott minden lehetséges esettel (üres halmaz, egyetlen pont, egy szakasz, egy háromszög, egy (konvex) négyszög, egy (konvex) ötszög), illetve az egyes alesetek vizsgálatába is számtalan kisebb-nagyobb hiba csúszott, ezért a sok részpontos megoldás.