Feladat:	B.4631	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Andi Gabriel Brojbeanu ,  Forrás Bence ,  Maga Balázs ,  Williams Kada
Füzet:	2017/március, 150 - 153. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Körök, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 2014/április: B.4631

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Kettő segédállítással kezdünk:   1. segédállítás: Tegyük fel, hogy a $c_1$ és $c_2$ körvonalak nem metszik egymást. Ekkor létezik olyan inverzió1, amely a $c_1$ és $c_2$ köröket koncentrikus körökbe képezi.   Az 1. segédállítás bizonyítása: Legyen $c_1$ középpontja $O_1$, $c_2$ középpontja $O_2$. Ha $O_1=O_2$, akkor bármilyen $O_1$ pólusú inverzió megfelel. Ha $O_1\ne O_2$, akkor legyen a $c_1$ és $c_2$ körök hatványvonala $h$. Mivel $c_1$ és $c_2$ nem metszi egymást, $h$ sem metszi a $c_1$ és $c_2$ körök egyikét sem. Legyen $H$ a $h$ hatványvonal tetszőleges pontja. A hatványvonal definíciója miatt $H$-ból a $c_1$ és $c_2$ körökhöz egyenlő hosszú érintők húzhatóak, jelöljük ezek közös hosszát $e$-vel, és tekintsük a $H$ középpontú, $e$ sugarú $c$ kört. Világos, hogy $c$ merőlegesen metszi $c_1$-et és $c_2$-t. Továbbá $c$ két pontban metszi az $f=O_1{O}_2$ centrális egyenest. Legyen ezen metszéspontok egyike $P$, $k$ pedig egy $P$ középpontú tetszőleges kör (1. ábra). 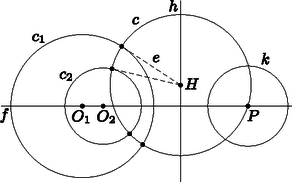  1. ábra   Megmutatjuk, hogy a $k$-ra vonatkozó inverzió a kívánalmaknak eleget tesz. Legyenek értelemszerűen a megfelelő körök és egyenesek $k$-ra vonatkozó inverz képei a $c_1\text{'}$ és $c_2\text{'}$ körök, valamint az $f\text{'}$ és $c\text{'}$ egyenesek. Az inverzió szögtartása miatt $f\text{'}$ és $c\text{'}$ merőlegesen metszi $c_1\text{'}$ és $c_2\text{'}$ mindegyikét, vagyis az egymástól különböző $f\text{'}$ és $c\text{'}$ egyenesek illeszkednek a $c_1\text{'}$ és $c_2\text{'}$ körök középpontjaira. Ebből következik, hogy a $c_1\text{'}$ és $c_2\text{'}$ körök középpontja közös, vagyis $c_1\text{'}$ és $c_2\text{'}$ koncentrikusak. Ezzel a segédállítást beláttuk.   1. megjegyzés: A gondolatmenetből kiolvasható, hogy a különböző $H$ középpontú körök szükségképpen ugyanabban a két pontban metszik az $e$ centrálist. A háttérben valójában a $c_1$ és $c_2$ körök által generált elliptikus körsor, valamint a rá ortogonális (más szóhasználattal hozzá konjugált) hiperbolikus körsor geometriája húzódik, amiről bővebben Hajós György: Bevezetés a geometriába c. könyvének 40. pontjában olvashatunk. 2. megjegyzés: Az állítás erősíthető, előírhatjuk, hogy a koncentrikus $c_1\text{'}$ és $c_2\text{'}$ körök közül melyik legyen a belső, és melyik a külső. Ehhez a két kapott lehetséges $P$ pont közül kell a megfelelőt kiválasztanunk. Ennek részletes belátását az olvasóra bízzuk, a továbbiakban csak azt fogjuk felhasználni, hogy ha $c_1$ belsejében van $c_2$, akkor elérhető, hogy $c_2\text{'}$ is $c_1\text{'}$ belsejében legyen; ehhez egy mindkét körön kívüli pólusra kell invertálni. 3. megjegyzés: Ha a $c_1$ és $c_2$ körök metszik egymást, nyilvánvalóan nincs olyan inverzió, amely őket koncentrikus körökbe képezi.   2. segédállítás: Legyen a $k$ kör középpontja $O$, $\ell$ egy $O$-ra illeszkedő egyenes, $A$, $B$, $C$ és $D$ pedig négy különböző, $O$-tól különböző pont $\ell$-en. A $k$-ra vonatkozó inverzió az $A$, $B$, $C$ és $D$ pontokat rendre az $A\text{'}$, $B\text{'}$, $C\text{'}$ és $D\text{'}$ pontokba képezi. Ekkor $\begin{array}{c}{\displaystyle \frac{AC}{CB}:\frac{AD}{DB}=\frac{A\text{'}C\text{'}}{C\text{'}B\text{'}}:\frac{A\text{'}D\text{'}}{D\text{'}B\text{'}}\mathrm{,}}\end{array}$ ahol az $\frac{XY}{YZ}$ arányhoz pozitív előjelet rendelünk, ha $Y\in \overline{XZ}$, egyébként pedig negatívat.   A 2. segédállítás bizonyítása: Válasszuk a koordinátarendszert úgy, hogy $O$ legyen az origó, $k$ sugara legyen egységnyi, és az $\ell$ egyenes egybeessen az $x$-tengellyel. Ekkor az állítás ekvivalens a könnyen ellenőrizhető $\begin{array}{c}{\displaystyle \frac{a-c}{c-b}:\frac{a-d}{d-b}=\frac{\frac{1}{a}-\frac{1}{c}}{\frac{1}{c}-\frac{1}{b}}:\frac{\frac{1}{a}-\frac{1}{d}}{\frac{1}{d}-\frac{1}{b}}}\end{array}$ azonossággal. Ezzel a 2. segédállítást beláttuk.   4. megjegyzés: A 2. segédállítás egy speciális esete annak a ténynek, hogy az inverzió tartja a kettősviszonyt, lásd Dobos Sándor, Hraskó András, Kiss Géza, Surányi László: Geometria, 11.‐12. évfolyam c. könyvében a 3.8. szakasz 3.2. és 3.3. feladatait, illetve Szőkefalvi-Nagy Béla: Komplex függvénytan c. könyvének 3. fejezetét.   Ezután rátérünk a feladat megoldására. Az állítás csak abban az esetben igaz, ha a négy érintkező kör közül $k_0$ a középső, először ezzel az esettel foglalkozunk. Legyen $k_4$ a $T_{12}{T}_{23}{T}_{31}$ kör. Világos, hogy $k_4$ a belsejében tartalmazza $k_0$-t, és merőlegesen metszi a $k_1$, $k_2$ és $k_3$ köröket. Tegyük fel, hogy $O\ne U$ és messe az $OU$ egyenes $k_4$-et az $A$ és $D$ pontokban, $k_0$-t a $B$ és $C$ pontokban a 2. ábra szerint. Az 1. segédállítást, illetve a 2. megjegyzést felhasználva hajtsunk végre egy alkalmas $P$ középpontú $k$ körre vonatkozó inverziót, amely a $k_0$ és $k_4$ köröket a koncentrikus $k_0\text{'}$ és $k_4\text{'}$ körökbe képezi, ahol $k_0\text{'}$ a $k_4\text{'}$ belsejében van. A $k_1$, $k_2$ és $k_3$ körök $k_1\text{'}$, $k_2\text{'}$ és $k_3\text{'}$ képei is körök lesznek, amelyek merőlegesen metszik $k_4\text{'}$-et, és kívülről érintik $k_0\text{'}$-t. Az $A$, $B$, $C$ és $D$ pontok egy $P$ pólusból induló félegyenesre illeszkednek, ezért $A\text{'}$, $B\text{'}$, $C\text{'}$ és $D\text{'}$ képeik is, de sorrendjük az eredetihez képest megfordul. Így az inverzió után a 3. ábrát kapjuk. 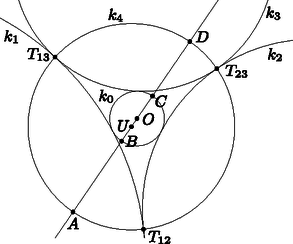  2. ábra 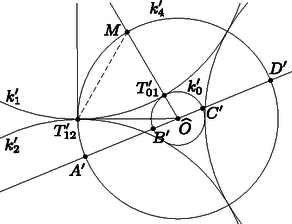    3. ábra   Használjuk a 3. ábra jelöléseit, $k_0\text{'}$ és $k_4\text{'}$ közös centruma legyen $\widehat{O}$. Mivel $k_1\text{'}$, $k_2\text{'}$ és $k_3\text{'}$ merőlegesen metszik $k_4\text{'}$-t, egymást páronként kívülről érintik, valamint érintik a $k_4\text{'}$-vel koncentrikus $k_0\text{'}$ kört, a sugaraik megegyeznek. Ebből könnyen látható, hogy $\widehat{O}\widehat{O_1}{T}_{12}\text{'}$ derékszögű háromszög $\widehat{O}$ szöge ${60}^{\circ }$, átfogójának felezőpontja $M$. Így $k_1\text{'}$ sugara egyrészt $\widehat{O_1}{T}_{01}\text{'}=2R\text{'}-r\text{'}$, másrészt $\widehat{O_1}{T}_{12}\text{'}=\sqrt[]{3}R\text{'}$, ahol $r\text{'}$ és $R\text{'}$ rendre $k_0\text{'}$ és $k_4\text{'}$ sugarát jelöli. Innen $r\text{'}=\left(2-\sqrt[]{3}\right)R\text{'}$ adódik, majd egyszerű számolással kapjuk, hogy $\begin{array}{c}{\displaystyle \frac{A\text{'}B\text{'}}{B\text{'}D\text{'}}:\frac{A\text{'}C\text{'}}{C\text{'}D\text{'}}=\frac{R\text{'}-r\text{'}}{R\text{'}+r\text{'}}:\frac{R\text{'}+r\text{'}}{R\text{'}-r\text{'}}={\left(\frac{\sqrt[]{3}-1}{3-\sqrt[]{3}}\right)}^2=\frac{1}{3}\mathrm{.}}\end{array}$ Most alkalmazzuk a 2. segédállítást, amiből következik, hogy $\begin{array}{c}{\displaystyle \frac{AB}{BD}:\frac{AC}{CD}=\frac{1}{3}\mathrm{.}}\end{array}$ (1) Bevezetve a $d=UV$ jelölést a 2. ábra szerint $AB=d+R-r$, $BD=R+r-d$, $AC=R+r+d$ és $CD=R-r-d$. Ezt visszahelyettesítve (1)-be nyerjük, hogy $\begin{array}{c}{\displaystyle \frac{R+d-r}{R+r-d}:\frac{R+r+d}{R-r-d}=\frac{1}{3}\mathrm{,}}\end{array}$ amiből a bizonyítandó $d^2=R^2-4Rr+r^2$ összefüggés egyszerű átszorzással következik. Hátra van az $O=U$ eset vizsgálata. Ekkor $d=0$ és az inverzió előtti ábránk lényegében megegyezik a 3. ábrával, így $r=\left(2-\sqrt[]{3}\right)R$, és $R^2-4Rr+r^2=0$ is azonnal következik. Ezzel azt az esetet beláttuk, amikor $k_0$ a középső kör. Ha $k_0$ nem a középső az adott négy páronként érintő kör közül, akkor az állítás nem igaz, de nagyon hasonló formula teljesül. Ez az eset az előzőhöz analóg módon kezelhető, ezért csak vázlatosan ismertetjük a lépéseket. A megfelelő inverzió után ismét a 3. ábrát kapjuk, ezért (1) továbbra is érvényes. Azonban ez esetben a 4.ábra szerint ${\displaystyle \begin{array}{c}\hfill {\displaystyle AB=R+d+r\mathrm{,}BD=d+r-R\mathrm{,}}\hfill \\ \hfill {\displaystyle AC=-r+d+R\text{ és }CD=d-r-R\mathrm{.}}\hfill \end{array}}$ Ezt (1)-be visszaírva, rendezés után a $d^2=R^2+4Rr+r^2$ összefüggést kapjuk. 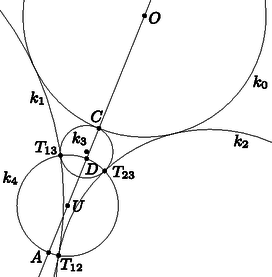  4. ábra   1Az inverzióról szóló ismertető cikket lásd honlapunkon: https://www.komal.hu/cikkek/cikklista.h.shtml.