Kezdőlap


Feladat:	B.4778	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Nguyen Viet Hung
Füzet:	2017/január, 21. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Körérintők
Hivatkozás(ok):	Feladatok: 2016/március: B.4778

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Használjuk az ábra jelöléseit. Jelölje $k_{A}$ és $k_{B}$ második metszéspontját $M$ , $k_{B}$ és $k_{C}$ metszéspontját $N$ , végül $k_{C}$ és $k_{A}$ metszéspontját $P$ . A Thalész-tétel miatt $A M D ∢ = B M D ∢ = 90^{\circ}$ , a két szög összege $180^{\circ}$ , tehát $B$ , $M$ és $A$ egy egyenesen vannak, vagyis az $M$ pont illeszkedik az $A B$ szakaszra. Ugyanígy látható be, hogy az $N$ pont a $B C$ , a $P$ pont pedig a $C A$ szakasz pontja.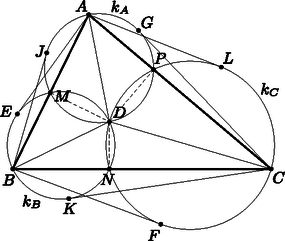

Írjuk fel sorra az

A

B

C

pontok őket nem tartalmazó másik két körre vonatkozó hatványait:

\begin{matrix} {A E}^{2} & = A M \cdot A B, \\ {A L}^{2} & = A P \cdot A C, \\ {B F}^{2} & = B N \cdot B C, \\ {B J}^{2} & = B M \cdot A B, \\ {C G}^{2} & = C P \cdot A C, \\ {C K}^{2} & = C N \cdot B C . \end{matrix}

Összegezve:

\begin{matrix} {A E}^{2} + {B J}^{2} + {B F}^{2} + {C K}^{2} + {A L}^{2} + {C G}^{2} = \\ = & (A M + B M) \cdot A B + (B N + C N) \cdot B C + (A P + C P) \cdot A C = \\ = & {A B}^{2} + {B C}^{2} + {A C}^{2} . \end{matrix}

Éppen a bizonyítandó állítást kaptuk.