Feladat:	B.4794	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Schrettner Jakab
Füzet:	2016/december, 539. oldal		PDF  |  MathML
Témakör(ök):	Egyéb poliéderek, Feladat, Térgeometriai számítások trigonometria nélkül, Térgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 2016/április: B.4794

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.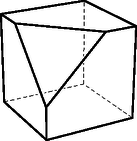   Megoldás. Jelölje a poliéder lapjainak számát $\ell$, éleinek számát $e$ és csúcsainak számát $c$. Ekkor Euler poliéderekre vonatkozó tétele alapján tudjuk, hogy $\begin{array}{c}{\displaystyle \ell +c=e+2.}\end{array}$ Minden csúcsba legalább 3 él fut, továbbá ha a csúcsok mentén megszámoljuk az éleket, akkor mindegyik élt kétszer számoljuk, vagyis $2e\ge 3c$. Fejezzük ki a lapok számát az Euler-tételből és használjuk fel az előbbi becslést: $\begin{array}{c}{\displaystyle \ell =2+e-c\ge 2+e-\frac{2}{3}e=2+\frac{1}{3}e\mathrm{.}}\end{array}$ A poliédernek a feladat szerint legalább 3 ötszöglapja van. Ez legalább 12 élt jelent, mert bármely 2 ötszöglapnak lehet egy közös éle. Innen már adódik, hogy $\ell \ge 6$. Azt is látjuk, hogy pontosan 6 lapja csak akkor lehet a poliédernek, ha legfeljebb 12 éle van. Egy 6 lapú, legfeljebb 12 élű poliédernek legfeljebb 8 csúcsa van a poliédertétel alapján. A 3 ötszöglapnak ennél több csúcsa van (bármely 2 ötszöglapnak 2 közös csúcsa lehet, tehát legalább $15-3\cdot 2=9$ csúcsuk van), vagyis a 6 lappal rendelkező ilyen poliédernek nem lehetne 3 ötszöglapja. A poliédernek tehát legalább 7 lapja van.     Pontosan 7 lappal konstruálható megfelelő poliéder, például ha egy téglatest egy csúcsát ,,levágjuk'' egy síkkal. Ennek a testnek három téglalap-, három ötszög- és egy háromszöglapja van.   Megjegyzések. 1. A versenyzők többféle konstrukciót adtak a megoldásaikhoz. A fenti mellett jellemző volt a következő is: Egy tetraéder három sarkát ,,vágjuk le'', így 1 hatszög-, 3 ötszög- és 3 háromszöglap keletkezik. 2. A http://www.komal.hu/verseny/feladat.cgi?a=feladat&f=B4794&l=hu linken látható két megoldás ettől különbözik. A feladatok megoldása általában pár nappal a határidő után honlapunkon megtalálható.