Kezdőlap


Feladat:	B.4789	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Horváth András János
Füzet:	2016/december, 538. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Szögfelező egyenes, Háromszög nevezetes körei
Hivatkozás(ok):	Feladatok: 2016/április: B.4789

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Legyen a beírt kör középpontja az $O$ pont, és használjuk a szokásos jelöléseket.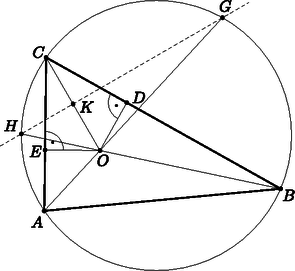

D

és

E

pontok érintési pontok, ezért

C D O ∢ = C E O ∢ = 90^{\circ}

. Ezek szerint a

D

és

E

pontok

O C

Thalesz-körén helyezkednek el, a kör középpontja, egyben a

D C E

háromszög köréírt körének középpontja, az

O C

szakasz

K

felezőpontja.
Az

A

B

G

C

H

pontok mind az

A B C

háromszög köréírt körén helyezkednek el, így többször felhasználhatjuk, hogy adott ívhez tartozó kerületi szögek mind egyenlők. Így

\begin{matrix} G H B ∢ & = G A B ∢ = \frac{α}{2}, A G H ∢ = A B H ∢ = \frac{β}{2}, \\ C H G ∢ & = C A G ∢ = \frac{α}{2}, H G C ∢ = H B C ∢ = \frac{β}{2} . \end{matrix}

Egy háromszög belső szögeinek összege

180^{\circ}

, így a

C H G

háromszögben

\begin{matrix} G C H ∢ = 180^{\circ} - \frac{α}{2} - \frac{β}{2}, \end{matrix}

továbbá az

O G H

háromszögben

\begin{matrix} H O G ∢ = 180^{\circ} - \frac{α}{2} - \frac{β}{2} . \end{matrix}

Beláttuk, hogy a

H O G

és

G C H

háromszögek egybevágók, mert szögeik páronként megegyeznek és egyik oldaluk (

G H

a leghosszabb oldal) közös. A

C H O G

négyszög tehát deltoid, amelynek szimmetriatengelye a

G H

átlója. Ez az átló így a másik átlót, az

O C

-t felezőpontjában, a

K

pontban metszi. Tehát a

G

K

H

pontok valóban egy egyenesre illeszkednek.