Kezdőlap


Feladat:	B.4780	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Varsányi András
Füzet:	2016/december, 535 - 537. oldal		PDF \| MathML
Témakör(ök):	Feladat, Szabályos sokszögek geometriája, Tengelyes tükrözés, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 2016/március: B.4780

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy az állítás pontosan akkor igaz, ha $n$ $1$ -nél nagyobb páratlan szám. A konvexségből következik, hogy ha a sokszög csúcsait $A_{1}, A_{2}, ..., A_{n}$ , az $A_{i} A_{i + 1}$ oldal felezőpontját pedig $F_{i}$ jelöli ( $i = 1,2, ..., n$ ), akkor $F_{1} F_{2} ... F_{n}$ is konvex $n$ -szög, és az $F_{i} F_{i + 1}$ egyenes által meghatározott két félsík közül $A_{i + 1}$ az egyikbe, az $A_{1} A_{2} ... A_{n}$ sokszög összes többi csúcsa pedig a másikba esik.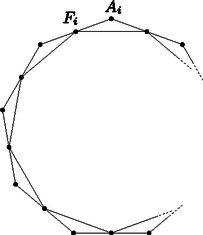

1. ábra

Ha adottak az oldalfelezőpontok és a sokszög

A_{1}

csúcsa, akkor ezek egyértelműen meghatározzák a sokszöget, mert az adott csúcsot sorban tükrözve az oldalfelezőpontokra megkapjuk az

n

-szög minden csúcsát. Ebből az is látszik, hogy a csúcs fixpontja annak a transzformációnak, amit az

F_{1}, F_{2}, ..., F_{n}

pontokra való egymás utáni tükrözések adnak meg. Tudjuk, hogy páratlan sok középpontos tükrözés egymásutánja megegyezik egy középpontos tükrözéssel, páros sok középpontos tükrözés egymásutánja pedig megegyezik egy eltolással (ami az identitás is lehet, ha az eltolás vektora

0

).
Ha tehát

n \geq 3

páratlan szám és az

F_{1} F_{2} ... F_{n}

sokszög szabályos, akkor

A_{1}

csak az a pont lehet, ami az

F_{1}, F_{2}, ..., F_{n}

pontokra való egymás utáni tükrözések által meghatározott középpontos tükrözés centruma, azaz az

A_{1}

pont egyértelműen létezik. Mivel egy szabályos sokszög oldalfelezőpontjai nyilván szabályos sokszöget határoznak meg, ezért

A_{1}

egyértelműsége azt jelenti, hogy az

A_{1} A_{2} ... A_{n}

sokszög is szabályos.
Ha viszont

n \geq 4

páros szám, akkor

A_{1}

bármely olyan pont lehet, ami az

F_{1}, F_{2}, ..., F_{n}

pontokra való egymás utáni tükrözések által meghatározott eltolásnak fixpontja. Most abból, hogy bármely szabályos sokszög oldalfelezőpontjai szabályos sokszöget határoznak meg, az következik, hogy a felezőpontokra való tükrözések egymásutánja a

0

vektorral való eltolás, azaz az identitás. Ennek minden pont fixpontja, tehát a sík tetszőleges

T

pontját sorban tükrözve a felezőpontokra, az

n

-edik tükrözés után visszajutunk a

T

pontba. Ha

T

-t úgy választjuk, hogy elég közel legyen annak a szabályos sokszögnek egy csúcsához, melynek oldalfelezőpontjai az

F_{1}, F_{2}, ..., F_{n}

pontok, akkor a tükrözések során kapott sokszög nyilván konvex lesz, de nem szabályos.
Ezzel állításunkat beláttuk.

II. megoldás. Használjuk az I. megoldás jelöléseit, továbbá legyenek egy rögzített

O

pontból a szereplő pontokba mutató helyvektorok a megfelelő kövér kisbetűkkel jelölve. Tudjuk, hogy bármely szakasz felezőpontjának helyvektora megegyezik a végpontok helyvektorainak számtani közepével. Ezért

\begin{matrix} f_{1} & = \frac{a_{1} + a_{2}}{2}, \\ f_{2} & = \frac{a_{2} + a_{3}}{2}, \\ ⋮ \\ f_{n - 1} & = \frac{a_{n - 1} + a_{n}}{2}, \\ f_{n} & = \frac{a_{n} + a_{1}}{2} . \end{matrix}

Minden második egyenletet

(- 1)

-gyel megszorozva, majd az egyenleteket összeadva kapjuk, hogy

\begin{matrix} f_{1} - f_{2} + f_{3} - ... + {(- 1)}^{n - 1} f_{n} = {\begin{matrix} a_{1}, & hanpáratlan, \\ 0, & hanpáros. \end{matrix} \end{matrix}

(1)

2. ábra

Ez azt jelenti, hogy ha

n \geq 3

páratlan, akkor a felezőpontok egyértelműen meghatározzák a csúcspontokat. Mivel egy szabályos

n

-szög oldalfelezőpontjai szabályos

n

-szöget alkotnak (hiszen az oldalfelezőpontok által meghatározott sokszöget megkapjuk, ha az eredeti sokszöget a középpontja körül

\frac{π}{n}

szöggel elforgatjuk és a középpontból

cos \frac{π}{n}

arányban kicsinyítjük, lásd a 2. ábrát), ezért ebben az esetben az eredeti sokszög szabályossága következik a felezőpontok által meghatározott sokszög szabályosságából. Ha

n \geq 4

páros, akkor viszont az (1) egyenlet szerint a felezőpontoknak eleget kell tenniük bizonyos feltételeknek (ha pl.

n = 4

, akkor könnyen látható, hogy (1) éppen azt a jól ismert tulajdonságot jelenti, mely szerint tetszőleges négyszög oldalfelezőpontjai paralelogrammát alkotnak), de a felezőpontok nem határozzák meg a csúcsokat. Ha ugyanis

b_{1}

egy tetszőleges pont helyvektora és

i = 1,2, ..., n - 1

esetén

b_{i + 1} = 2 f_{i} - b_{i}

, akkor

\begin{matrix} b_{i} = 2 (f_{i - 1} - f_{i - 2} + ... + {(- 1)}^{i} f_{1}) + {(- 1)}^{i + 1} b_{1} . \end{matrix}

Ezért

i < n

esetén a

B_{i} B_{i + 1}

szakasz felezőpontja nyilván

F_{i}

, az pedig, hogy

B_{n} B_{1}

felezőpontja

F_{n}

, az (1) egyenletből következik, mert azt felhasználva kapjuk, hogy

\begin{matrix} b_{n} & = 2 (f_{n - 1} - f_{n - 2} + ... + {(- 1)}^{n} f_{1}) + {(- 1)}^{n + 1} b_{1} = \\ = 2 ((f_{n} - f_{n}) + f_{n - 1} - f_{n - 2} + ... + f_{1}) - b_{1} = \\ = 2 f_{n} - 2 \cdot 0 - b_{1} = 2 f_{n} - b_{1} . \end{matrix}

B_{1}

-et úgy választjuk, hogy elég közel legyen

A_{1}

-hez, akkor a

B_{1} B_{2} ... B_{n}

sokszög nyilván konvex lesz. Tehát ha

n

páros, akkor végtelen sok olyan nem szabályos konvex

n

-szög létezik, melyek oldalfelezőpontjai szabályos

n

-szöget alkotnak.
Vagyis a feladatban szereplő állítás akkor igaz, ha

n

1

-nél nagyobb páratlan szám.