Feladat:	2016. évi Nemzetközi Matematika Diákolimpia 23. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Gáspár Attila
Füzet:	2016/november, 454 - 455. oldal		PDF  |  MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia, Ponthalmazok, Indirekt bizonyítási mód
Hivatkozás(ok):	Feladatok: 2016/szeptember: 2016. évi Nemzetközi Matematika Diákolimpia 23. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Gáspár Attila megoldása. Rajzoljunk egy olyan nagy kört, ami az összes szakaszt tartalmazza a belsejében. Hosszabbítsuk meg az összes szakaszt úgy, hogy a végpontjaik a körre kerüljenek. Két szakasz legfeljebb egy pontban metszheti egymást, ezért nem jön létre új metszéspont, tehát a hosszabbítás semmit nem befolyásol. Nevezzük a szakaszvégpontokat belépési és kilépési pontoknak attól függően, hogy indul-e belőle béka, vagy nem. Nyilvánvaló, hogy $n$ db belépési és $n$ db kilépési pont van. Tegyük fel, hogy a körön van két szomszédos belépési pont. Az 1. ábrán látható, a két szakasz metszéspontig tartó részei és a köztük lévő, más pontot nem tartalmazó körív által határolt alakzat legyen $X$. Látható, hogy mindegyik szakasz (az $X$-et határoló szakaszokat kivéve) 0 vagy 2 pontban metszi az $X$ határvonalát, mert az $X$ konvex. A körívet egyik sem metszi, ezért mindegyik a két szakaszt fogja metszeni. A két $X$-et határoló szakaszon így ugyanannyi metszéspont lesz, ez legyen $y$. Mivel $y\le n-2$, ezért $y+1$ ugrás után a két béka összeütközik. Ez ellentmondás, tehát nem lehet két szomszédos belépési pont. Ha a békák $n-1$ helyett $n$-szer ugranak, akkor a kilépési pontokba érkeznek. Ilyenkor nem történhet ütközés, ezért ez nem módosítja a feladatot. Nyilvánvaló, hogy ha a békák nem ütköztek, akkor a kilépési pontokból indulva sem ütköznének, ekkor a lépéssorozat visszafelé játszódna le. Ebből következik, hogy nem lehet két szomszédos kilépési pont. Így a körön lévő pontok felváltva kilépési és belépési pontok. 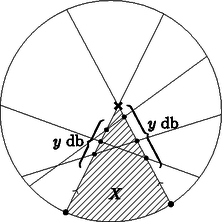  1. ábra   $a)$ Válasszunk ki egy végpontot, és legyen belépési pont. A többi végpont felváltva legyen kilépési és belépési pont. Egy tetszőleges szakaszt az összes többi metsz, ezért a két oldalán ugyanannyi végpont van. Összesen $2n$ végpont van, ezért egy oldalon $n-1$ db van. Ez páros, ezért a szakasz végpontjai különböző típusúak (2. ábra). 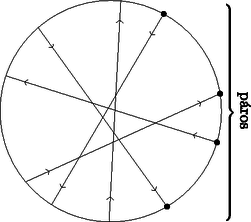  2. ábra   Tegyük fel, hogy van két béka, ami összeütközik. Legyen a 3. ábrán látható, a két szakasz metszéspontig tartó részei és a két belépési pontot összekötő, a két szakasz kilépési pontját nem tartalmazó körív által határolt alakzat $X$. Az $X$ konvex, ezért minden szakasz 0 vagy 2 pontban metszi az $X$ határvonalát. A két béka ütközik, ezért a két szakasz határvonalán ugyanannyi metszéspont van. A köríven páratlan számú végpont van, mert két belépési pont között vannak. Így összesen páratlan számú pontban metszik a szakaszok az $X$ határvonalát. Ez ellentmondás, tehát a békák nem ütköznek. 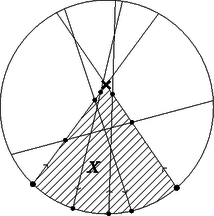  3. ábra   $b)$ Tegyük fel, hogy lehetséges. Egy szakasz egyik oldalán $n-1$ végpont van. Ez páratlan, ezért a szakasz két végpontja ugyanolyan típusú. Ez ellentmondás (4. ábra). 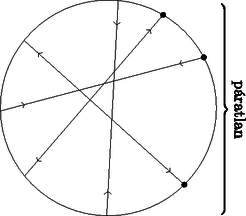  4. ábra