Feladat:	2016. évi Nemzetközi Matematika Diákolimpia 11. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Williams Kada
Füzet:	2016/október, 386 - 387. oldal		PDF  |  MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia, Síkgeometriai bizonyítások, Hatványvonal, hatványpont, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 2016/szeptember: 2016. évi Nemzetközi Matematika Diákolimpia 11. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Williams Kada megoldása. A bonyolult ábra miatt célszerű egy jól megszerkesztett ábrán minden újonnan felvett pontra megvizsgálni, milyen tulajdonságai vannak. Miután az ábra rejtelmeit kiismertük, a befejezés önként fog adódni. A szögszámításhoz legyen $\begin{array}{c}{\displaystyle BAC\sphericalangle =CAD\sphericalangle =ACD\sphericalangle =DAE\sphericalangle =ADE\sphericalangle =\alpha \mathrm{,}}\end{array}$ ezek egyenlőségét a $D$ és $E$ pont definíciója indokolja. Ekkor $BFC\sphericalangle =FBA\sphericalangle +FAB\sphericalangle =2\alpha$. A kerületi, illetve kerületi és középponti szögek tételét és azok megfordítását KT, illetve KKT rövidíti. A következő lépésekben igazoljuk a feladat állítását: 1. Az $ABC$ kör középpontja $D$. 2. $B$, $C$, $D$, $F$ egy $k$ körre illeszkedik. 3. $ABCD\sim AFDE$. 4. $B$, $F$, $E$ egy egyenesen van. 5. $A$, $B$, $M$, $D$, $E$ egy $\ell$ körre illeszkedik. 6. Az $X$ pont is a $k$ körön van. 7. $MXEF$ húrtrapéz, körülírt köre $m$. 8. A hatványpont-tételt $k$, $\ell$, $m$ körökre alkalmazva készen vagyunk. Az egyes lépések belátása lényegében csak szögszámítás, így érdemes magának az Olvasónak megpróbálni ellenőrizni őket. A lépések indoklása alább olvasható: 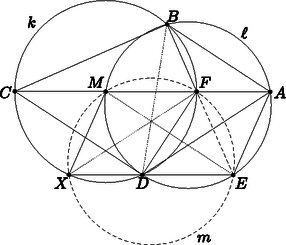    1. $ABC\sphericalangle ={90}^{\circ }+\alpha$ és $ADC\sphericalangle ={180}^{\circ }-2\alpha$ (mert $DA=DC$). KKT miatt $D$ csakis az $ABC$ kör középpontja lehet. 2. Ez KT-vel adódik: $BFC\sphericalangle =2\alpha =BDC\sphericalangle$, utóbbi az $ABC$ körre vett KKT miatt. 3. A $k$ körbeli KT-ből $CDF\sphericalangle ={90}^{\circ }$, így $AFD\sphericalangle =CDF\sphericalangle +DCF\sphericalangle ={90}^{\circ }+\alpha$. Innen két szög egyezése miatt $ABC\sim AFD$, de $ADC\sim AED$ miatt $ABCD\sim AFDE$ is igaz. 4. Mivel $DA=DB$ (1. lépés), a hasonlóságból $EA=EF$, s így $EFA\sphericalangle =2\alpha =BFC\sphericalangle$, vagyis $BF$ és $FE$ egyenes egybeesik. 5. $CBF\sphericalangle ={90}^{\circ }$ lévén $\overline{CF}$ a $k$ átmérője, $M$ így $k$ középpontja. Innen világos, hogy $MBF\sim DBA\sim EFA$, mert $2\alpha$ alapon fekvő szögű egyenlő szárú háromszögek. A 4. lépés miatt $BMA\sphericalangle =BDA\sphericalangle =BEA\sphericalangle$ adódik, és így KT szerint $A$, $B$, $M$, $D$, $E$ egy körön van. 6. $EDA\sphericalangle =DAC\sphericalangle =\alpha$ lévén $DE\parallel AC$, vagyis $E$, $D$, $X$ kollineáris. $AMXE$ paralelogrammából $MXD\sphericalangle =MAE\sphericalangle =2\alpha$, és az $\ell$ körbeli KT-ből $MDE\sphericalangle ={180}^{\circ }-MAE\sphericalangle$, amiért $MDX\sphericalangle =2\alpha$. Tehát $MD=MX$, azaz $X$ a $k$ körön van. 7. Az $AMXE$ paralelogrammából az $EFA$ egyenlő szárú háromszöget kivágva egy húrtrapézt kapunk, az $MXEF$ húrtrapézt. 8. A $k$ és $\ell$ körök hatványvonala $BD$, a $k$ és $m$ köröké $FX$, az $\ell$ és $m$ köröké pedig $ME$. A hatványpont-tétel szerint e három egyenes egy pontra illeszkedik vagy párhuzamos. Nyilván nem párhuzamosak, ezért egy ponton mennek át.   Megjegyzés. Adható két másik, szintén tanulságos megközelítés, ami elsősorban nem köröket vizsgál. Kulcsészrevétel az 1‐3. lépések után, hogy $BCDF$ és $AFD$ körök sugara egyenlő, hisz $FD$ közös húrjukhoz mindkettőben $\alpha$ kerületi szög tartozik. Az adódó egyenlő szakaszokból az alábbi befejezések kínálkoznak: $\left(a\right)$ $ME$-re tükrözve $B\mathrm{,}D$ képe $X\mathrm{,}F$ lesz, így $BD$ és $FX$ az $ME$ szimmetriatengelyen metsz; $\left(b\right)$ Az $MXEF$ húrtrapéz átlói oly szögűek, hogy a $BMF$ körön messék egymást, így szimmetria miatt az $MF$ ív felezőpontjára illeszkednek, akárcsak az $MBF$ szög $BD$ szögfelezője.