Kezdőlap


Feladat:	2011. évi Kürschák matematikaverseny 3. feladata	Korcsoport: -	Nehézségi fok: -
Megoldó(k):	Fleiner Tamás
Füzet:	2012/február, 70 - 71. oldal		PDF \| MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd), Síkbeli ponthalmazok távolsága, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 2012/február: 2011. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megjegyzés. A megoldáshoz vezető alábbi ötletre sokan rájöttek. Ha igaz az állítás, akkor annak úgy is teljesülnie kell, ha az adott egyenesek mindegyike ugyanazon az $O$ ponton halad át, és ugyanez a metszéspont van $2 n$ multiplicitással megadva. Ha ekkor egy $O$ -tól különböző $P$ pont rendelkezik a kívánt tulajdonsággal, akkor az $O P$ félegyenes bármely pontja ilyen tulajdonságú. Márpedig, ha ,,kellően messziről'' nézünk rá a síkra, akkor az egyenesek és a pontok ,,nagyon közel'' lesznek ehhez az állapothoz. Az utolsó ötlet pedig az, hogy ha nagyon sok egyenes van adva, és azok egy szabályos $6 n$ oldalú sokszög átmérői, akkor $P$ -nek az egyenesektől mért össztávolsága ,,nagyjából'' arányos lesz az $O P$ távolsággal. Tehát ha az állítás igaz, akkor annak már egy véletlenül választott $P$ pontra is pozitív valószínűséggel kell teljesülnie. Ezeket a gondolatokat bontjuk ki az alábbi megoldásban.

Megoldás. Válasszunk egy olyan

k

kört a síkon, amiből a

3 n

egyenes mindegyike olyan húrt metsz ki, amihez legalább

(1 - \frac{1}{10 n}) π

nagyságú középponti szög tartozik. Könnyen látható, hogy létezik ilyen kör: válasszuk a

k

kör

O

középpontját tetszőlegesen, sugara pedig

\begin{matrix} r = d \cdot cos ((\frac{10 n - 1}{20 n}) π) \end{matrix}

legyen, ahol

d

az adott egyeneseknek az

O

-tól mért távolságai közül a legnagyobb.
Ha

H

egy, a

k

körbe írt szabályos hatszög és

e

a megadott egyenesek egyike, akkor azt mondjuk, hogy

H

jó

e

-hez, ha

H

-nak

3 - 3

csúcsa esik

e

mindkét partjára, azaz

e

H

két átellenes oldalát metszi. A

k

választása folytán az olyan szabályos hatszögek csúcsai, amik nem jók

e

-hez a

k

körnek hat ívét alkotják, és mindegyik ívhez legfeljebb

\frac{π}{10 n}

nagyságú középponti szög tartozik. Mivel

6 \cdot 3 n

ilyen ív nem fedheti a

k

kört, ezért található olyan

k

-ba írt

P_{1} P_{2} P_{3} P_{4} P_{5} P_{6}

szabályos hatszög, ami a megadott

3 n

egyenes mindegyikéhez jó. Sőt, még az is feltehető, hogy a

3 n

egyenes egyike sem merőleges a

P_{1} P_{2} P_{3} P_{4} P_{5} P_{6}

hatszög egyetlen oldalára sem.
Azt állítjuk, hogy a

P_{1}

P_{2}

P_{3}

P_{4}

P_{5}

P_{6}

pontok valamelyike rendelkezik a feladatban leírt tulajdonsággal. Ehhez elegendő megmutatni, hogy e hat pontnak a

2 n

megadott ponttól vett távolságösszege több, mint a

3 n

egyenestől vett távolságösszege, hiszen ekkor nem lehetséges hogy mindegyik

P_{i}

-nek a pontoktól mért távolságösszege legalább akkora legyen, mint az egyenesektől való. Legyen tehát

X

a megadott pontok valamelyike. A háromszög-egyenlőtlenség miatt

\begin{matrix} | \bar{P_{1} X} | + | \bar{P_{4} X} | \geq | \bar{P_{1} P_{4}} | = 2 r, \end{matrix}

hisz

P_{1}

és

P_{4}

r

sugarú

k

kör átellenes pontjai. Hasonló okból

\begin{matrix} | \bar{P_{2} X} | + | \bar{P_{5} X} | \geq | \bar{P_{2} P_{5}} | = 2 r és | \bar{P_{3} X} | + | \bar{P_{6} X} | \geq | \bar{P_{3} P_{6}} | = 2 r, \end{matrix}

tehát

\begin{matrix} | \bar{P_{1} X} | + | \bar{P_{2} X} | + | \bar{P_{3} X} | + | \bar{P_{4} X} | + | \bar{P_{5} X} | + | \bar{P_{6} X} | \geq 6 r . \end{matrix}

A megadott pontok mindegyikére összeadva a fenti becslést azt kapjuk, a

P_{i}

pontoknak a

2 n

megadott ponttól vett távolságösszege legalább

12 r n

. A bizonyítás befejezéséhez az alábbiakban azt igazoljuk, hogy a

P_{i}

pontoknak az egyenesektől mért távolságösszege kisebb

12 r n

-nél.
Legyen

e

a megadott

3 n

egyenes valamelyike. Feltehetjük, hogy

e

P_{1} P_{6}

és

P_{3} P_{4}

oldalakat metszi, azaz

e

egyik partján a

P_{1}

P_{2}

és

P_{3}

, míg a másikon a

P_{4}

P_{5}

és

P_{6}

pontok vannak. Világos, hogy a

P_{1}

és

P_{6}

pontoknak az

e

egyenestől mért távolságainak összege megegyezik a

\bar{P_{1} P_{6}}

szakasznak egy

e

-re merőleges

f

egyenesre vett merőleges vetületének hosszával.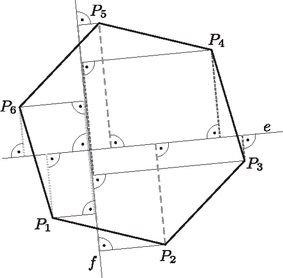

Hasonlóan, a

P_{2}

és

P_{5}

, illetve a

P_{3}

és

P_{4}

pontok

e

-től mért távolságösszege a

\bar{P_{2} P_{5}}

, illetve a

\bar{P_{3} P_{4}}

szakaszok

f

-re vett merőleges vetületének hossza. Márpedig a merőleges vetület hossza sosem nagyobb a vetített szakaszénál, jelen esetben pedig szigorúan kisebb annál, ugyanis a hatszöget úgy választottuk, hogy

P_{1} P_{6}

nem merőleges

e

-re. Tehát a kérdéses távolságösszeg szigorúan kisebb, mint e három szakasz összhossza, azaz

| \bar{P_{1} P_{6}} | + | \bar{P_{2} P_{5}} | + | \bar{P_{3} P_{4}} | = r + 2 r + r = 4 r

, hiszen a szabályos hatszög oldalhossza megegyezik a köré írt kör sugarával, míg az átellenes csúcsokat összekötő húr a

k

kör átmérője.
Azt kaptuk, hogy a

P_{i}

-knek a megadott

3 n

egyenestől a távolságösszege kisebb, mint

3 n \cdot 4 r = 12 r n

. Nekünk pedig pontosan ezt kellett bizonyítanunk.

□

Megjegyzés. A feladatbelinél erősebb állítás is igaz. Ha nem csak egy szabályos hatszög csúcsaival dolgozunk, hanem egy megfelelően nagy

k

körön egyenletes eloszlással választott véletlen pontra számítjuk ki a kérdéses távolságösszegek várható értékeit (ehhez a

k

kör mentén kell integrálni), akkor az is könnyen igazolható, hogy tetszőleges

n

pont és

k

egyenes esetén, ahol

k < \frac{π}{2} \cdot n

, mindig létezik olyan

P

pont a síkon, hogy

P

-nek a pontoktól vett távolságösszege legalább akkora, mint

P

-nek az egyenesektől mért távolságainak összege.