Kezdőlap


Feladat:	2010. évi Kürschák matematikaverseny 2. feladata	Korcsoport: -	Nehézségi fok: -
Megoldó(k):	Fleiner Tamás
Füzet:	2011/február, 69 - 70. oldal		PDF \| MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd), Matematika, Síkgeometriai bizonyítások, Ceva-tétel
Hivatkozás(ok):	Feladatok: 2011/február: 2010. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A jól ismert Ceva-tétel trigonometrikus alakját fogjuk használni, amely szerint az $A A^{*}$ , $B B^{*}$ és $C C^{*}$ egyenesek pontosan akkor mennek át egy ponton, ha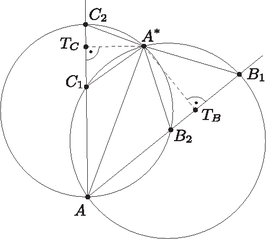

\begin{matrix} \frac{sin B A A^{*} ∢}{sin C A A^{*} ∢} \cdot \frac{sin A C C^{*} ∢}{sin B C C^{*} ∢} \cdot \frac{sin C B B^{*} ∢}{sin A B B^{*} ∢} = 1. \end{matrix}

Az első tört kiszámításához figyeljük meg, hogy

A B_{2} A^{*} C_{2}

húrnégyszög, ezért

A C_{2} A^{*} ∢ = A^{*} B_{2} B_{1} ∢

; továbbá

A B_{1} A^{*} ∢ = A^{*} C_{1} C_{2} ∢

, hiszen

A B_{1} A^{*} C_{1}

is húrnégyszög.
A megfelelő szögek egyenlősége miatt tehát

A^{*} C_{1} C_{2} ▵ \sim A^{*} B_{1} B_{2} ▵

, így a megfelelő oldalak aránya megegyezik a hozzájuk tartozó magasságok arányával, vagyis

\begin{matrix} \frac{| B_{1} B_{2} |}{| C_{1} C_{2} |} = \frac{| A^{*} T_{B} |}{| A_{*} T_{C} |}, \end{matrix}

ahol rendre

T_{B}

, illetve

T_{C}

jelöli az

A^{*}

-ból az

A B

, illetve

A C

egyenesekre bocsátott merőlegesek talppontjait. Tudjuk még, hogy

\begin{matrix} sin B A A^{*} ∢ = \frac{| A^{*} T_{B} |}{| A A^{*} |}, illetve sin C A A^{*} ∢ = \frac{| A^{*} T_{C} |}{| A A^{*} |}, \end{matrix}

ezért

\begin{matrix} \frac{sin B A A^{*} ∢}{sin C A A^{*} ∢} = \frac{| A^{*} T_{B} |}{| A^{*} T_{C} |} = \frac{| B_{1} B_{2} |}{| C_{1} C_{2} |} . \end{matrix}

Hasonlóan látható be, hogy

\begin{matrix} \frac{sin A C C^{*} ∢}{sin B C C^{*} ∢} = \frac{| A_{1} A_{2} |}{| B_{1} B_{2} |}, illetve \frac{sin C B B^{*} ∢}{sin A B B^{*} ∢} = \frac{| C_{1} C_{2} |}{| A_{1} A_{2} |} . \end{matrix}

A Ceva-tételben szereplő szorzatra tehát

\begin{matrix} \frac{sin B A A^{*} ∢}{sin C A A^{*} ∢} \cdot \frac{sin A C C^{*} ∢}{sin B C C^{*} ∢} \cdot \frac{sin C B B^{*} ∢}{sin A B B^{*} ∢} = \frac{| B_{1} B_{2} |}{| C_{1} C_{2} |} \cdot \frac{| A_{1} A_{2} |}{| B_{1} B_{2} |} \cdot \frac{| C_{1} C_{2} |}{| A_{1} A_{2} |} = 1 \end{matrix}

adódik, és nekünk pontosan ezt kellett bizonyítanunk.

□