Kezdőlap


Feladat:	B.4684	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Andó Angelika , Cseh Kristóf , Csépai András , Döbröntei Dávid Bence , Fekete Panna , Kovács Márton , Molnár-Sáska Zoltán , Nagy-György Pál , Schrettner Bálint , Schwarcz Tamás , Szebellédi Márton , Varga-Umbrich Eszter , Williams Kada
Füzet:	2016/május, 274 - 276. oldal		PDF \| MathML
Témakör(ök):	Feladat, Egyenesek egyenlete, Síkgeometriai bizonyítások, Körülírt kör
Hivatkozás(ok):	Feladatok: 2015/január: B.4684

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Legyenek az $E$ pontból az oldalakra állított merőlegeseknek a szemközti oldalakkal vett metszéspontjai $P$ , $Q$ , $R$ és $S$ , a merőlegesek talppontjai pedig $P_{0}$ , $Q_{0}$ , $R_{0}$ és $S_{0}$ , az ábra szerint.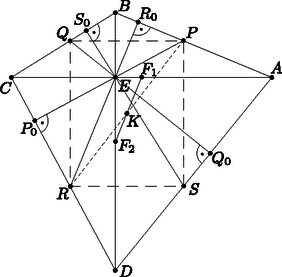

E

pontból merőlegeseket állítottunk az oldalakra, így a

B R_{0} E S_{0}

C S_{0} E P_{0}

D P_{0} E Q_{0}

és

A Q_{0} E R_{0}

négyszögek két-két szemközti szöge derékszög, tehát húrnégyszögek.
Belátjuk, hogy a

P

R_{0}

S_{0}

P_{0}

pontok egy körön vannak. A

B E C

derékszögű háromszög átfogóhoz tartozó magassága

E S_{0}

, ezért

B E S_{0} ∢ = B C E ∢

. Másrészt mivel

B R_{0} E S_{0}

és

C S_{0} E P_{0}

húrnégyszögek:

\begin{matrix} B R_{0} S_{0} ∢ = B E S_{0} ∢ = B C E ∢ = S_{0} P_{0} E ∢ . \end{matrix}

S_{0} P_{0} E ∢

P R_{0} S_{0} P_{0}

négyszög belső szöge, míg a

B R_{0} S_{0} ∢

a szemközti csúcshoz tartozó külső szög. A négyszög valóban húrnégyszög.
Hasonló gondolatmenettel igazoljuk, hogy

R_{0} S_{0} P_{0} R

szintén húrnégyszög. A

B C E

háromszögben ‐ az előző esetnek megfelelően ‐ az átfogóhoz tartozó magasság két hasonló derékszögű háromszögre bontja a háromszöget, így felhasználva az előbbi két húrnégyszöget is:

\begin{matrix} S_{0} R_{0} E ∢ = S_{0} B E ∢ = S_{0} E C ∢ = S_{0} P_{0} C ∢ . \end{matrix}

R_{0} S_{0} P_{0} R

négyszög

R_{0}

-hoz tartozó belső szöge egyenlő a

P_{0}

-hoz tartozó külső szöggel, tehát ez a négyszög is húrnégyszög.
Abból, hogy a

D P_{0} E Q_{0}

négyszög húrnégyszög, az is következik, hogy

\begin{matrix} E P_{0} Q_{0} ∢ = E D Q_{0} ∢ . \end{matrix}

D E A

derékszögű háromszögben

E Q_{0}

magasság, így

E D Q_{0} ∢ = Q_{0} E A ∢

. Mivel

A Q_{0} E R_{0}

húrnégyszög, azért

Q_{0} E A ∢ = Q_{0} R_{0} A ∢

. Mindezekből:

\begin{matrix} P P_{0} Q_{0} ∢ = E P_{0} Q_{0} ∢ = E D Q_{0} ∢ = Q_{0} E A ∢ = Q_{0} R_{0} A ∢ = Q_{0} R_{0} P ∢, \end{matrix}

tehát

P R_{0} P_{0} Q_{0}

húrnégyszög.
Az eddigiekből következik, hogy a

P

R_{0}

S_{0}

P_{0}

R

és

Q_{0}

pontok egy körön vannak.
Ugyanígy belátható, hogy a

Q

P_{0}

S

Q_{0}

R_{0}

és

S_{0}

pontok is egy körre illeszkednek.
Tehát mind a nyolc pont,

Q

P_{0}

R

S

Q_{0}

P

R_{0}

és

S_{0}

egy körön van.
Következő lépésként igazoljuk, hogy a

P Q R S

négyszög oldalai párhuzamosak az

A B C D

négyszög átlóival. A négy párhuzamosság közül egyet fogunk megmutatni, a másik három analóg módon tárgyalható.
Az előző részben már több négyszögről láttuk, hogy húrnégyszög, sőt azt is sikerült igazolni, hogy a nyolc pont egy körön van. Emiatt

R_{0} S_{0} Q R

húrnégyszög. A

C Q R ∢

külső szög, egyenlő a szemközti csúcshoz,

R_{0}

-hoz tartozó belső szöggel, az

S_{0} R_{0} E

szöggel. Mivel

B R_{0} E S_{0}

húrnégyszög kapjuk, hogy

\begin{matrix} S_{0} R_{0} E ∢ = S_{0} B E ∢ = C B D ∢ . \end{matrix}

C Q R ∢

és a

C B D ∢

tehát egyenlők, és mivel egyik száruk közös, azért egyállású szögek:

Q R

párhuzamos

B D

-vel. A fentiekből kapjuk, hogy a

P Q R S

négyszög téglalap, amelynek oldalai párhuzamosak az

A B C D

négyszög átlóival.
A megoldás befejezéséhez be kell még bizonyítani, hogy a téglalap átlóinak metszéspontja illeszkedik az

A B C D

négyszög átlóinak felezőpontját összekötő szakaszra. Ezt az állítást, kihasználva az

A B C D

négyszög átlóinak merőlegességét, vektorok segítségével igazoljuk.
Legyen az

A

B

C

D

P

Q

R

S

pontokba mutató helyvektorok kezdőpontja

E

, az

A B C D

négyszög átlóinak metszéspontja. Legyen

\begin{matrix} \vec{E A} = a, \vec{E C} = λ a, \vec{E B} = b és \vec{E D} = μ b, \end{matrix}

ahol

λ

és

μ

negatív valós számok. Ismert, hogy amennyiben

P

A B

szakasz belső pontja, az

\vec{E P}

helyvektor kifejezhető a csúcsokba mutató

a

és

b

helyvektorok segítségével úgy, hogy

\begin{matrix} \vec{E P} = x \cdot a + (1 - x) b, \end{matrix}

ahol az

x \in] 0,1 [

. A

P Q

szakasz párhuzamos

A C

-vel, így az

\vec{E Q}

vektort felbontva

b

-vel és

λ a

-val párhuzamos összetevőkre a

b

együtthatója meg kell, hogy egyezzen az előzővel:

\begin{matrix} \vec{E Q} = (1 - x) \cdot b + x \cdot λ a . \end{matrix}

Innen már a további két csúcsba mutató helyvektorok felírása is azonnal adódik:

\begin{matrix} \vec{E R} & = x \cdot λ a + (1 - x) \cdot μ b, \\ \vec{E S} & = (1 - x) \cdot μ b + x \cdot a . \end{matrix}

A C

átló

F_{1}

felezőpontjára és a

B D

átló

F_{2}

felezőpontjára:

\begin{matrix} \vec{E F_{1}} & = \frac{1}{2} (a + λ a), \\ \vec{E F_{2}} & = \frac{1}{2} (b + μ b) . \end{matrix}

Vegyük most az

F_{1} F_{2}

szakaszt és legyen ennek a szakasznak az

(1 - x) : x

arányban osztó, belső pontja

K

. Ekkor a

K

pont helyvektora:

\begin{matrix} \vec{E K} = x \cdot \vec{E F_{1}} + (1 - x) \cdot \vec{E F_{2}} = \frac{1}{2} (x (1 + λ) a + (1 - x) (1 + μ) b) . \end{matrix}

Végül tekintsük a

P Q R S

téglalap átlóinak közös felezőpontját. Ennek helyvektora az átló végpontjaiba mutató helyvektorok öszegének a fele, pl.:

\begin{matrix} \frac{1}{2} \vec{E P} + \frac{1}{2} \vec{E R} = \frac{1}{2} (x \cdot a + (1 - x) b) + \frac{1}{2} (x \cdot λ a + (1 - x) \cdot μ b) = \vec{E K} . \end{matrix}

Ezzel az állítást igazoltuk.