Feladat:	B.4673	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gál Boglárka ,  Geng Máté ,  Imolay András ,  Keresztfalvi Bálint ,  Khayouti Sára ,  Kocsis Júlia ,  Nagy-György Pál ,  Németh Balázs ,  Szebellédi Márton ,  Szőke Tamás ,  Vághy Mihály ,  Williams Kada
Füzet:	2016/május, 272 - 274. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Húrnégyszögek, Síkgeometriai bizonyítások, Körülírt kör
Hivatkozás(ok):	Feladatok: 2014/december: B.4673

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.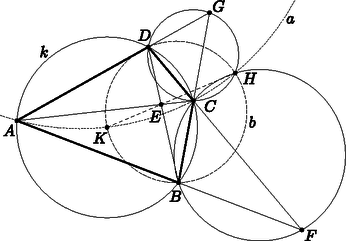   Megoldás. Először azt látjuk be, hogy a $G$, $H$, $F$ pontok egy egyenesbe esnek.     $FHCB$ húrnégyszög, mivel mindegyik pontja rajta van a $BFC$ háromszög köré írt körén. Hasonlóan $HGDC$ is húrnégyszög. Mindebből ${\displaystyle \begin{array}{cc}\hfill {\displaystyle FHC\sphericalangle }& {\displaystyle ={180}^{\circ }-FBC\sphericalangle =CBA\sphericalangle \mathrm{,}}\hfill \\ \hfill {\displaystyle CHG\sphericalangle }& {\displaystyle ={180}^{\circ }-GDC\sphericalangle =CDA\sphericalangle \mathrm{.}}\hfill \end{array}}$ $CBA\sphericalangle +CDA\sphericalangle ={180}^{\circ }$, hiszen $ABCD$ húrnégyszög. Tehát $FHC\sphericalangle +CHG\sphericalangle ={180}^{\circ }$, így a $G$, $H$, $F$ pontok valóban egy egyenesbe esnek. Most belátjuk, hogy a $HCKA$, illetve a $HDKB$ négyszögek húrnégyszögek. Az $ABCD$ húrnégyszög megváltoztatásával bizonyos szögek megváltozhatnak, de az, hogy a két négyszög húrnégyszög ekkor is analóg módon bizonyítható. (Ilyen eset lehet, ha például a $K$ pont átkerül az $AC$ szakasz $B$-vel átellenes oldalára.) Ehhez a $CKA\sphericalangle +AHC\sphericalangle ={180}^{\circ }$, illetve a $DKB\sphericalangle +BHD\sphericalangle ={180}^{\circ }$ feltételeket kell igazolnunk. A kerületi és középponti szögek tétele miatt: $\begin{array}{c}{\displaystyle CKA\sphericalangle =2\cdot CBA\sphericalangle =2\beta \mathrm{,}\text{valamint}DKB\sphericalangle =2\cdot DAB\sphericalangle =2\alpha \mathrm{.}}\end{array}$ Tehát elegendő belátnunk, hogy: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle AHC\sphericalangle }& {\displaystyle ={180}^{\circ }-2\beta \text{és}BHD\sphericalangle ={180}^{\circ }-2\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle AHC\sphericalangle }& {\displaystyle ={180}^{\circ }-\left(FHC\sphericalangle +AHG\sphericalangle \right)\mathrm{,}BHD\sphericalangle ={180}^{\circ }-\left(FHB\sphericalangle +DHG\sphericalangle \right)\mathrm{.}}\hfill \end{array}}$ Most pedig igazoljuk, hogy: $\begin{array}{c}{\displaystyle FHB\sphericalangle =DHG\sphericalangle =\alpha \mathrm{,}FHC\sphericalangle =AHG\sphericalangle =\beta \mathrm{.}}\end{array}$ $FHB\sphericalangle =FCB\sphericalangle$ az $FHCB$ húrnégyszögben, és $\begin{array}{c}{\displaystyle FCB\sphericalangle ={180}^{\circ }-BCD\sphericalangle =DAB\sphericalangle =\alpha \mathrm{.}}\end{array}$ Ugyanígy $DHG\sphericalangle =DCG\sphericalangle ={180}^{\circ }-BCD\sphericalangle =DAB\sphericalangle =\alpha$. A másik szögpárnál szükségünk lesz még egy húrnégyszögre, a $BHGA$ négyszögre. Ez a négyszög is húrnégyszög, hiszen $\begin{array}{c}{\displaystyle BHG\sphericalangle ={180}^{\circ }-BHF\sphericalangle ={180}^{\circ }-BCF\sphericalangle =BCD\sphericalangle ={180}^{\circ }-DAB\sphericalangle \mathrm{,}}\end{array}$ és így $GAB\sphericalangle +BHG\sphericalangle ={180}^{\circ }$. Tehát $GABH$ húrnégyszög, így: $\begin{array}{c}{\displaystyle AHG\sphericalangle =ABG\sphericalangle =ABC\sphericalangle =\beta \mathrm{.}}\end{array}$ Mivel $FHCB$ húrnégyszög: $\begin{array}{c}{\displaystyle CHF\sphericalangle ={180}^{\circ }-FBC\sphericalangle =ABC\sphericalangle =\beta \mathrm{.}}\end{array}$ Tehát igazoltuk, hogy a $HCKA$ és a $HDKB$ négyszögek húrnégyszögek, így rátérhetünk a bizonyítandó állításra. Legyen a $HCKA$ négyszög köré írt köre $a$, $HDKB$-é $b$, $ABCD$-é pedig $k$. Végezzünk $k$ alapkörű inverziót1, mely során $a$-t és $b$-t invertáljuk. Mindkét kör képe egyenes lesz, hiszen ezen körök átmennek $k$ középpontján, $K$-n. Másrészről, mivel $A$, $B$, $C$, $D$ egyaránt $k$ pontjai, az inverzió ezeket helyben hagyja. Tehát $a$ képe egy egyenes, mely átmegy az $A$ és $C$ pontokon ‐ ez éppen az $AC$ egyenes. Hasonlóan $b$ képe a $BD$ egyenes lesz. Ezek metszéspontja $E$. Az $a$ és $b$ invertálása során kaptunk egy olyan pontot, mely $a$ és $b$ inverzén is rajta van. Az inverzió két különböző ponthoz két különböző pontot rendel. Ez azt jelenti, hogy $E$ az $a$ és $b$ közös pontjának inverze lesz. Az $a$ és $b$ két közös ponttal rendelkezik: $H$-val és $K$-val. Közülük $K$ az alapkör középpontja, melynek nincs inverze. Ebből következik, hogy $H$ inverze $E$, vagyis $K$, $H$ és $E$ egy egyenesen van. 1Az I. 324. feladat az inverzió bemutatása volt prezentáció segítségével: http://www.komal.hu/verseny/feladat.cgi?a=feladat&f=I324&l=hu.