Feladat:	B.4710	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Czirkos Angéla
Füzet:	2016/április, 215 - 216. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Ponthalmazok, Körök, Logikai feladatok
Hivatkozás(ok):	Feladatok: 2015/április: B.4710

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Megmutatjuk, hogy van olyan egységsugarú zárt körlemez, amely legalább három $\text{P}$-beli pontot tartalmaz. A megoldás során tetszőleges $A$ pont esetén $k_A$ az $A$ középpontú egységsugarú zárt körlemezt jelöli. Először azt látjuk be, hogy van két olyan $\text{P}$-beli pont, melyek távolsága kisebb, mint $2$. Legyen $P_1\in \text{P}$ tetszőleges halmazbeli pont, $Q$ pedig olyan pont, melyre $P_{1}Q=1$. Ekkor $k_Q$ nem tartalmazza a belsejében $P_1$-et, ezért a feltételek szerint van olyan $P_2\in \text{P}$ pont, melyet $k_Q$ a belsejében tartalmaz. Ekkor $P_1{P}_2$ rövidebb, mint $k_Q$ átmérője, azaz $P_1{P}_2<2$ (1. ábra).   1. ábra   Ezért van olyan $R$ pont (a $P_1$, illetve $P_2$ középpontú 1 sugarú körvonalak két metszéspontja közül az egyik), melyre $R{P}_1=R{P}_2=1$. Tehát $k_R$ nem tartalmazza a belsejében sem $P_1$-et, sem $P_2$-t, ezért a feltételek szerint van olyan $P_3\in \text{P}$ pont, melyet $k_R$ a belsejében tartalmaz (2. ábra). Vagyis $k_R$ tartalmazza a $P_1$, $P_2$ és $P_3$ pontok mindegyikét, s ezzel állításunkat beláttuk. 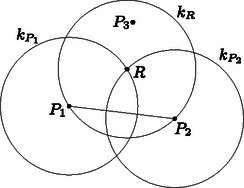  2. ábra