Feladat:	B.4683	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Barabás Ábel ,  Baran Zsuzsanna ,  Cseh Kristóf ,  Csépai András ,  Fekete Panna ,  Lajkó Kálmán ,  Nagy-György Pál ,  Schwarcz Tamás ,  Szebellédi Márton ,  Vághy Mihály ,  Williams Kada
Füzet:	2016/április, 212 - 215. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Szabályos sokszög alapú gúlák, Térgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 2015/január: B.4683

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Megmutatjuk, hogy a válasz mindkét esetben igen. Belátjuk, hogy bármely szabályos ötszög alapú egyenes gúlához létezik olyan sík, amely a gúlát olyan hatszögben metszi, mely tengelyesen is és középpontosan is szimmetrikus. Legyen a gúla alapja az egységnyi oldalú $ABCDE$ szabályos ötszög, hatodik csúcsa pedig $F$. Tudjuk, hogy a szabályos ötszög minden szöge ${108}^{\circ }$, átlóinak hossza pedig az oldalak hosszának $\left(\sqrt[]{5}+1\right)/2$-szerese. Legyen az $AE$ és $CD$ egyenesek metszéspontja $M$, a $BC$ és $ED$ egyenesek metszéspontja pedig $N$ (1. ábra). Ekkor 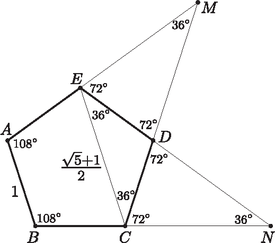$DEM\sphericalangle =EDM\sphericalangle ={180}^{\circ }-{108}^{\circ }={72}^{\circ }$. Tehát ${\displaystyle \begin{array}{cc}\hfill {\displaystyle EMD\sphericalangle }& {\displaystyle ={180}^{\circ }-2\cdot {72}^{\circ }={36}^{\circ }=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{{180}^{\circ }-{108}^{\circ }}{2}=ECD\sphericalangle \mathrm{,}}\hfill \end{array}}$ ezért a $CEM$ háromszög egyenlőszárú, s így $EM=EC=\left(\sqrt[]{5}+1\right)/2$. Az ötszög szimmetriája miatt ebből $CN=DN=DM=\left(\sqrt[]{5}+1\right)/2$ is következik.   1. ábra   Az $AB$ szakasz $\text{T}$ felezőmerőleges síkja tartalmazza $D$-t és $F$-et, $C$ és $E$, illetve $N$ és $M$ pedig egymásnak $\text{T}$-re vonatkozó tükörképei. Legyen $0\le \lambda \le 1$ valós szám, $U_{\lambda }$, illetve $V_{\lambda }$ a $CD$, illetve az $ED$ szakasznak az a pontja, melyre $C{U}_{\lambda }=\lambda =E{V}_{\lambda }$. Ekkor $U_{\lambda }$ és $V_{\lambda }$ is egymásnak $\text{T}$-re vonatkozó tükörképei. Legyen ${\text{S}}_{\lambda }$ az $U_{\lambda }{V}_{\lambda }$ egyenest tartalmazó, az $FNM$ síkkal párhuzamos sík. Mivel $U_{\lambda }{V}_{\lambda }$ merőleges $\text{T}$-re, ezért ${\text{S}}_{\lambda }$ is merőleges $\text{T}$-re. Legyen ${\text{S}}_{\lambda }$ és a gúla $FE$, $FA$, $FB$ és $FC$ éleinek metszéspontja rendre $W_{\lambda }$, $Z_{\lambda }$, $X_{\lambda }$ és $Y_{\lambda }$ (2. ábra). Ekkor $W_{\lambda }$ és $Y_{\lambda }$, valamint $Z_{\lambda }$ és $X_{\lambda }$ is egymásnak $\text{T}$-re vonatkozó tükörképei, tehát az $U_{\lambda }{V}_{\lambda }{W}_{\lambda }{Z}_{\lambda }{X}_{\lambda }{Y}_{\lambda }$ hatszög szimmetrikus $\text{T}$-re, s ezért tengelyesen is szimmetrikus a $\text{T}\cap {\text{S}}_{\lambda }$ egyenesre. Vagyis az ${\text{S}}_{\lambda }$ sík minden $0<\lambda <1$ esetén tengelyesen szimmetrikus hatszögben metszi a gúlát. 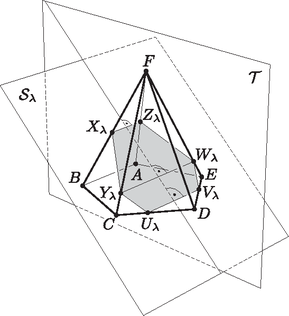  2. ábra   Megmutatjuk, hogy van olyan $\lambda$ érték, melyre a metszet középpontosan is szimmetrikus. Tudjuk, hogy három sík páronkénti metszésvonalai vagy egy ponton mennek át, vagy párhuzamosak. (Ennek az állításnak a bizonyítása megtalálható pl. Geometriai feladatok gyűjteménye I, 1703. feladat.) Tekintsük az $FBC$, $FDE$ és ${\text{S}}_{\lambda }$ síkokat. Ezek páronkénti metszésvonalai $BC\cap ED=N$ miatt $FN$, továbbá $X_{\lambda }{Y}_{\lambda }$ és $V_{\lambda }{W}_{\lambda }$. E három egyenesnek nem lehet közös pontja, mert $FN$ párhuzamos a másik két egyenest tartalmazó ${\text{S}}_{\lambda }$ síkkal. Tehát az $X_{\lambda }{Y}_{\lambda }$ és $V_{\lambda }{W}_{\lambda }$ egyenesek párhuzamosak. Ugyanígy kapjuk az $FCD$, $FEA$ és ${\text{S}}_{\lambda }$ síkok páronkénti metszésvonalainak vizsgálatából, hogy az $FM$, $W_{\lambda }{Z}_{\lambda }$ és $Y_{\lambda }{U}_{\lambda }$ egyenesek is párhuzamosak (3. ábra). 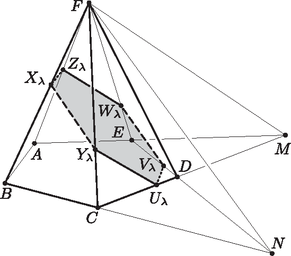  3. ábra   Ha $\lambda =0$, akkor $V_0\equiv W_0\equiv E$, a hatszög egy négyszöggé fajul. Mivel $W_0{Z}_0$ párhuzamos $FM$-mel, ezért a párhuzamos szelők tétele szerint $\begin{array}{c}{\displaystyle \frac{W_0{Z}_0}{MF}=\frac{EA}{MA}\mathrm{,}\text{azaz}{W}_0{Z}_0=\frac{EA}{MA}\cdot MF=\frac{1}{1+\frac{\sqrt[]{5}+1}{2}}MF=\frac{3-\sqrt[]{5}}{2}MF\mathrm{.}}\end{array}$ Ha $\lambda =1$, akkor $U_1\equiv V_1\equiv D$, a hatszög egy ötszöggé fajul. Mivel $V_1{W}_1=D{W}_1$ párhuzamos $FN$-mel, ezért a párhuzamos szelők tétele, valamint a szabályos ötszög szimmetriája miatt $\begin{array}{c}{\displaystyle \frac{D{W}_1}{NF}=\frac{DE}{NE}=\frac{EA}{MA}\mathrm{,}\text{azaz}D{W}_1=\frac{3-\sqrt[]{5}}{2}NF=\frac{3-\sqrt[]{5}}{2}MF\mathrm{.}}\end{array}$ Tehát az $FEA$ és az $FDE$ háromszögek egybevágósága miatt kapjuk, hogy $F{Z}_0=F{W}_1$. Ezért a $Z_0$ és $W_1$ pontok az $FAE$ egyenlőszárú háromszög szárain szimmetrikusan helyezkednek el. Legyen $Z_{0}EA\sphericalangle =W_{1}AE\sphericalangle =\alpha$. Viszont $Z_1{W}_1$ párhuzamos $FM$-mel, s így $Z_{0}E$-vel is, ha tehát $Z_1{W}_1\cap AM=P$, akkor $Z_{1}PA\sphericalangle =\alpha$. Ha $FA{W}_1\sphericalangle =\beta$, akkor felhasználva, hogy $Z_1{W}_{1}A\sphericalangle =2\alpha$ (mert a $W_{1}AP$ háromszög külső szöge), valamint azt, hogy ${90}^{\circ }>FAE\sphericalangle =\alpha +\beta$, kapjuk, hogy $\begin{array}{c}{\displaystyle A{Z}_1{W}_1\sphericalangle ={180}^{\circ }-\beta -2\alpha >\beta =Z_{1}A{W}_1\sphericalangle \mathrm{.}}\end{array}$ Mivel bármely háromszögben nagyobb szöggel szemben nagyobb oldal van, ezért ebből az következik, hogy $W_1{Z}_1<A{W}_1$, vagyis $A{W}_1=E{Z}_0=W_0{Z}_0=V_1{W}_1$ miatt $W_1{Z}_1<V_1{W}_1$. Azt már láttuk, hogy $0=V_0{W}_0<V_1{W}_1=W_0{Z}_0$. Ha $\lambda$ folytonosan nő $0$-tól $1$-ig, akkor a párhuzamos szelők tétele miatt $V_{\lambda }{W}_{\lambda }=\lambda \cdot V_1{W}_1$ is folytonosan nő $0$-tól $V_1{W}_1$-ig, $W_{\lambda }{Z}_{\lambda }$ pedig folytonosan csökken $W_0{Z}_0$-tól $W_1{Z}_1$-ig. Mivel $W_1{Z}_1<V_1{W}_1$, ezért lesz egy olyan $\lambda$ érték, melyre $V_{\lambda }{W}_{\lambda }=W_{\lambda }{Z}_{\lambda }$ teljesül. (A párhuzamos szelők tételének többszöri alkalmazásával kiszámolható, hogy $\lambda =\frac{5+\sqrt[]{5}}{10}$ esetén lesz egyenlőség, lásd a megoldás utáni Megjegyzést.) Ha $V_{\lambda }{W}_{\lambda }=W_{\lambda }{Z}_{\lambda }$, akkor a hatszög tengelyes szimmetriájából következő $V_{\lambda }{W}_{\lambda }=Y_{\lambda }{U}_{\lambda }$ és $W_{\lambda }{Z}_{\lambda }=X_{\lambda }{Y}_{\lambda }$ egyenlőségek miatt miatt azt kapjuk, hogy a hatszög két-két szemközti oldalpárja, $V_{\lambda }{W}_{\lambda }$ és $X_{\lambda }{Y}_{\lambda }$, valamint $Y_{\lambda }{U}_{\lambda }$ és $W_{\lambda }{Z}_{\lambda }$ nemcsak párhuzamos, hanem egyenlő hosszú is. Ez azt jelenti, hogy a $V_{\lambda }{W}_{\lambda }{X}_{\lambda }{Y}_{\lambda }$ és az $Y_{\lambda }{U}_{\lambda }{W}_{\lambda }{Z}_{\lambda }$ négyszögek paralelogrammák. Ezért átlóik felezik egymást. Vagyis ha a $W_{\lambda }{Y}_{\lambda }$ szakasz felezőpontja $O$, akkor a $V_{\lambda }{X}_{\lambda }$ és $U_{\lambda }{Z}_{\lambda }$ szakaszok felezőpontja is $O$. Ez pedig azt jelenti, hogy az $U_{\lambda }{V}_{\lambda }{W}_{\lambda }{Z}_{\lambda }{X}_{\lambda }{Y}_{\lambda }$ hatszög az $O$ pontra nézve középpontosan szimmetrikus. Ezzel állításunkat beláttuk. 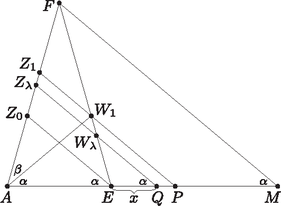  Megjegyzés. $\lambda$ pontos értékét a 4. ábra jelöléseit használva számoljuk ki. Legyen az ${\text{S}}_{\lambda }$ sík és az $AM$ egyenes döféspontja $Q$, jelöljük az $EQ$ távolságot $x$-szel. Ekkor egyrészt ${\displaystyle \begin{array}{cc}\hfill {\displaystyle W_{\lambda }{Z}_{\lambda }}& {\displaystyle =Q{Z}_{\lambda }-Q{W}_{\lambda }=\frac{AQ}{AM}\cdot MF-\frac{EQ}{EM}\cdot MF}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left(\frac{1+x}{\frac{\sqrt[]{5}+3}{2}}-\frac{x}{\frac{\sqrt[]{5}+1}{2}}\right)MF=\frac{3-\sqrt[]{5}+\left(4-2\sqrt[]{5}\right)x}{2}MF\mathrm{.}}\hfill \end{array}}$ Másrészt az $EC$-vel párhuzamos $U_{\lambda }{V}_{\lambda }$ egyenes is átmegy $Q$-n, ezért $E{V}_{\lambda }Q\sphericalangle ={36}^{\circ }$, tehát az $E{V}_{\lambda }Q$ és $EMD$ háromszögek hasonlóak, ezért $E{V}_{\lambda }=\frac{\sqrt[]{5}+1}{2}EQ$, s így $\begin{array}{c}{\displaystyle W_{\lambda }{V}_{\lambda }=\frac{E{V}_{\lambda }}{EN}\cdot NF=\frac{\frac{\sqrt[]{5}+1}{2}x}{\frac{\sqrt[]{5}+3}{2}}NF=\frac{\left(\sqrt[]{5}-1\right)x}{2}NF\mathrm{.}}\end{array}$ Mivel $MF=NF$, ezért $W_{\lambda }{Z}_{\lambda }=W_{\lambda }{V}_{\lambda }$ pontosan akkor teljesül, ha $\begin{array}{c}{\displaystyle \frac{3-\sqrt[]{5}+\left(4-2\sqrt[]{5}\right)x}{2}=\frac{\left(\sqrt[]{5}-1\right)x}{2}\mathrm{,}}\end{array}$ azaz ha $x=\sqrt[]{5}/5$. Ebből pedig azt kapjuk, hogy $\begin{array}{c}{\displaystyle \lambda =E{V}_{\lambda }=\frac{\sqrt[]{5}+1}{2}x=\frac{\sqrt[]{5}+1}{2}\cdot \frac{\sqrt[]{5}}{5}=\frac{5+\sqrt[]{5}}{10}\approx 0\mathrm{,}7236.}\end{array}$   4. ábra