Kezdőlap


Feladat:	B.4708	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Nagy Dávid Paszkál
Füzet:	2016/március, 148 - 149. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Oldalfelező merőleges, Háromszög nevezetes körei, Magasságpont
Hivatkozás(ok):	Feladatok: 2015/április: B.4708

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Legyen az

A B C

háromszög magasságvonalainak a

k

körülírt körrel való, a csúcsoktól különböző metszéspontja rendre

A_{2}

B_{2}

és

C_{2}

. Mivel

A A_{2}

k

kör

B C

-re merőleges húrja, ezért ennek

f_{a}

felezőmerőlegese átmegy

O

-n és merőleges

B C

felezőmerőlegesére is. Vizsgáljuk meg, mi lesz

A_{2}

-nek az

O

-ra vonatkozó tükörképe. Ismert, hogy egy pontra vonatkozó középpontos tükrözés helyettesíthető két olyan egyenesre vonatkozó tengelyes tükrözés egymásutánjával, melyek egymást merőlegesen metszik az adott pontban. Ezért ha

A_{2}

-t tükrözzük

f_{a}

-ra, majd a képét,

A

-t,

B C

felezőmerőlegesére, akkor a kapott

A_{1}

pont megegyezik

A_{2}

-nek az

O

-ra vonatkozó tükörképével (1. ábra). Ugyanígy látható be, hogy a

B_{2}

, illetve

C_{2}

pontok

O

-ra vonatkozó tükörképe

B_{1}

, illetve

C_{1}

1. ábra

Tehát az

A_{1} B_{1} C_{1}

háromszög

O

-ra vonatkozó tükörképe az

A_{2} B_{2} C_{2}

háromszög. Ezért

K

-nak az

O

-ra vonatkozó tükörképe megegyezik az

A_{2} B_{2} C_{2}

háromszög beírt körének

L

középpontjával. Mivel

O

nyilván felezi az

L K

szakaszt, ezért feladatunk állításának igazolásához elegendő megmutatnunk, hogy

M \equiv L

, ami ekvivalens azzal, hogy az

A_{2} B_{2} C_{2}

háromszögben az

A B C

háromszög magasságvonalai belső szögfelezők.
Legyen az

A B C

háromszög

A

-nál lévő szöge

α

. Mivel

B B_{2} ⊥ A C

és

C C_{2} ⊥ A B

, ezért

A B B_{2} ∢ = 90^{\circ} - α = A C C_{2} ∢

. A

k

körben a kerületi szögek tétele miatt

A A_{2} B_{2} ∢ = A B B_{2} ∢

és

A A_{2} C_{2} ∢ = A C C_{2} ∢

, tehát

A A_{2} B_{2} ∢ = A A_{2} C_{2} ∢

(2. ábra). Vagyis

A A_{2}

felezi a

C_{2} A_{2} B_{2}

szöget. Ugyanígy látható be, hogy

B B_{2}

és

C C_{2}

is szögfelezők, s ezzel feladatunk állítását igazoltuk.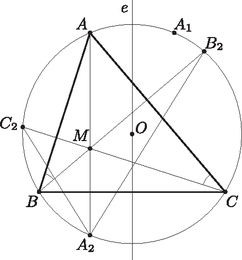

2. ábra