Feladat: B.4693 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Czirkos Angéla 
Füzet: 2016/március, 147 - 148. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Síkgeometriai bizonyítások, Síkgeometriai számítások trigonometriával
Hivatkozás(ok):Feladatok: 2015/február: B.4693

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Legyen KBC∢=α. Ekkor a feltételek szerint ABK∢=2α. E szögek segítségével felírva az ABK és KBC háromszögek területét, kapjuk hogy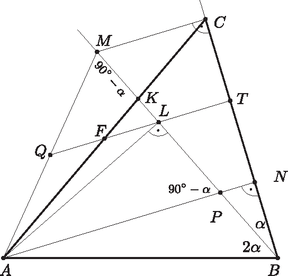

TABK=AB⋅BK⋅sin2α2,   valamintTKBC=BK⋅BC⋅sinα2.
A két háromszög B csúcshoz tartozó magassága közös, B-vel szemközti oldalaik aránya pedig 2:1, mert K az AC oldal harmadolópontja. Ezért TABK:TKBC=2:1. Ebből a sin2α=2sinαcosα azonosságot is felhasználva kapjuk, hogy
AB⋅BK⋅sinαcosα=BK⋅BC⋅sinα,
vagyis (sinα≠0 miatt) cosα=BCAB.

 
 

Legyen M a B-ből induló BK félegyenesnek az a pontja, melyre BM=BA. Ekkor cosα=BCBM, ezért BCM∢=90∘. Továbbá az ABM háromszög egyenlőszárú, szárszöge 2α, ezért alapon fekvő szögei MAB∢=AMB∢=90∘-α.
Legyen az A-ból BC-re állított merőleges talppontja N, az AN és BK szakaszok metszéspontja pedig P. A PNB derékszögű háromszög egyik hegyesszöge α, ezért a másik hegyesszög BPN∢=90∘-α. Ekkor MPA∢=90∘-α is, mert MPA∢ és BPN∢ csúcsszögek, tehát egyenlőek. Ez azt jelenti, hogy az APM háromszög is egyenlőszárú, mert M-nél és P-nél lévő szögei megegyeznek. Ezért az alaphoz tartozó magassága, AL, felezi az MP alapot, tehát L az MP szakasz felezőpontja.
Legyen az AM szakasz felezőpontja Q. Ekkor QL az APM, QF pedig az AMC háromszög középvonala. A középvonalak párhuzamosak a háromszögek megfelelő oldalaival, azaz AP-vel, illetve MC-vel. E két utóbbi viszont egymással is párhuzamos, mert mindkettő merőleges BC-re. Tehát QF és QL is merőlegesek BC-re. Vagyis a Q-ból BC-re állított merőleges tartalmazza F-et és L-et is, ezért FL is merőleges BC-re, ami épp a bizonyítandó állítás.