Feladat:	B.4682	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Andó Angelika ,  Baran Zsuzsanna ,  Csépai András ,  Fekete Panna ,  Gáspár Attila ,  Katona Dániel ,  Kovács Péter Tamás ,  Lajkó Kálmán ,  Mócsy Miklós ,  Molnár-Sáska Zoltán ,  Nagy Dávid Paszkál ,  Nagy-György Pál ,  Németh Balázs ,  Schrettner Bálint ,  Szebellédi Márton ,  Szőke Tamás ,  Tóth Viktor ,  Williams Kada
Füzet:	2016/március, 145 - 146. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Kombinatorikus geometria, Teljes indukció módszere, Indirekt bizonyítási mód
Hivatkozás(ok):	Feladatok: 2015/január: B.4682

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Megmutatjuk, hogy $m=2k$. Először azt látjuk be, hogy ha van olyan egyenes, amelyik a $3k$ pont közül legalább $\left(2k+1\right)$-et tartalmaz, akkor a pontok nem oszthatók $k$ darab hármas csoportba úgy, hogy az egy csoportban lévő pontok egy háromszög csúcsai. Ez azonnal következik abból, hogy tetszőleges háromszög három csúcsa közül egy egyenes legfeljebb kettőt tartalmaz, ezért $k$ darab különböző háromszög csúcsai közül legfeljebb $2k$ darabot tartalmazhat bármely egyenes. Ha nincs olyan egyenes, amelyik $2k$-nál többet tartalmaz a $3k$ pont közül, akkor $k$ szerinti teljes indukcióval megmutatjuk, hogy a pontok $k$ darab hármas csoportba oszthatók úgy, hogy az egy csoportban lévő pontok egy háromszög csúcsai. Ha $k=1$, akkor a feltételünk szerint a három pont nem kollineáris, ezért egy háromszög csúcsait alkotja, tehát ekkor igaz az állítás. A $k=2$ esetet is külön bizonyítjuk, mert az indukciós lépés során fel fogjuk használni, hogy a pontok száma legalább 6. Ha a pontok közül semelyik három nem kollineáris, akkor bárhogyan is osztjuk őket két csoportba, az egy csoportban lévő pontok egy háromszög csúcsai lesznek. Ha a pontok közül pontosan négy, mondjuk $A$, $B$, $C$ és $D$ egy $e$ egyenesre esik, a maradék kettő, $E$ és $F$ pedig nincs rajta $e$-n, akkor például $\left\{A\mathrm{,}B\mathrm{,}E\right\}$, $\left\{C\mathrm{,}D\mathrm{,}F\right\}$ jó beosztás (1. ábra). Végül ha a pontok közül semelyik négy nem kollineáris, de mondjuk $A$, $B$ és $C$ egy $e$ egyenesre esik, akkor a maradék három pont közül válasszunk ki kettőt, legyenek ezek $D$ és $E$. Feltehető, hogy a $DE$ és $e$ egyenesek metszéspontja nem $A$. Ekkor ha a hatodik pont $F$, akkor például $\left\{A\mathrm{,}D\mathrm{,}E\right\}$, $\left\{B\mathrm{,}C\mathrm{,}F\right\}$ jó beosztás (2. ábra). 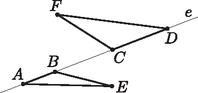  1. ábra 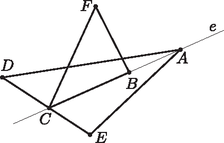    2. ábra   Tegyük fel, hogy az állítás igaz $k=n>1$-re. Legyen adott $3\left(n+1\right)$ különböző pont úgy, hogy közülük legfeljebb $2\left(n+1\right)$ esik egy egyenesbe. Tekintsük azokat az egyeneseket, melyek a pontok közül legalább kettőt tartalmaznak. Legyen ezek száma $N$. (Az ilyen egyenesek száma véges, hiszen nyilván fennáll az $N\le \left(\genfrac{}{}{0ex}{}{3n+3}{2}\right)$ egyenlőtlenség.) Jelölje ezeket az egyeneseket ${\ell }_1\mathrm{,}{\ell }_2\mathrm{,}\text{...}\mathrm{,}{\ell }_N$, és válasszuk úgy a számozást, hogy ha $|{\ell }_i|$ az adott pontok közül azoknak a száma, melyeket az ${\ell }_i$ egyenes tartalmaz, akkor minden $i=\mathrm{1,2,}\text{...}\mathrm{,}N-1$ esetén teljesüljön az $|{\ell }_i|\ge |{\ell }_{i+1}|$ egyenlőtlenség (a számozás nem egyértelmű, mert lehetnek olyan egyenesek, melyek ugyanannyi pontot tartalmaznak). Először megmutatjuk, hogy $|{\ell }_3|<2n+1$. Tegyük fel, hogy ez nem igaz. Ha $|{\ell }_3|\ge 2n+1$, akkor $|{\ell }_2|\ge 2n+1$ és $|{\ell }_1|\ge 2n+1$ is fennáll. Ezért e három egyenes az adott pontok közül legalább $3\left(2n+1\right)-3=6n$ különbözőt tartalmaz, hiszen az egyeneseken lévő pontok közül legfeljebb az ${\ell }_1\cap {\ell }_2$, ${\ell }_1\cap {\ell }_3$ és ${\ell }_2\cap {\ell }_3$ pontokat számoltuk kétszer a $3\left(2n+1\right)$ összegben (3. ábra). Viszont $n>1$ miatt $6n>3n+3$, s ebből az ellentmondásból következik, hogy $|{\ell }_3|<2n+1$. Hasonló módon látjuk be, hogy $|{\ell }_2|<2n+2$. Ha ugyanis $|{\ell }_2|\ge 2n+2$, akkor $|{\ell }_1|\ge 2n+2$, ezért e két egyenes az adott pontok közül legalább $2\left(2n+2\right)-1=4n+3>3n+3$ különbözőt tartalmaz, hiszen az egyeneseken lévő pontok közül legfeljebb az ${\ell }_1\cap {\ell }_2$ pontot számoltuk kétszer a $2\left(2n+2\right)$ összegben. Ebből az ellentmondásból következik, hogy 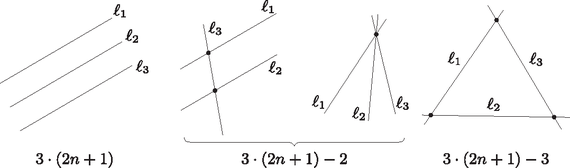$|{\ell }_2|<2n+2$.   3. ábra   Tehát $|{\ell }_1|\le 2n+2$, $|{\ell }_2|\le 2n+1$, és ha $i>2$, akkor $|{\ell }_i|\le 2n$ teljesül. Válasszunk ki az ${\ell }_1$ egyenesen lévő adott pontok közül kettőt tetszőlegesen, és vegyünk hozzájuk harmadiknak az ${\ell }_2$ egyenesen lévő adott pontok közül egy olyat, amelyik nincs rajta az ${\ell }_1$ egyenesen. E három pont nyilván háromszöget alkot. A maradék $\left(3n+3\right)-3=3n$ pontra pedig teljesül az indukciós feltevésünk, mert közülük semelyik $2n$ nincs egy egyenesen. Hiszen továbbra is csak az ${\ell }_i$ egyenesek tartalmaznak a pontok közül legalább kettőt, az ${\ell }_1$-en lévő maradék pontok száma legfeljebb $\left(2n+2\right)-2=2n$, az ${\ell }_2$-en lévő maradék pontok száma legfeljebb $\left(2n+1\right)-1=2n$, a többi egyenesre pedig $|{\ell }_i|\le 2n$ teljesül. Vagyis ezek a pontok beoszthatók $n$ darab hármas csoportba úgy, hogy az egy csoportban lévő pontok egy háromszög csúcsai. Ezért a $3n+3$ pont is beosztható a feltételeknek megfelelően, s ezzel állításunkat beláttuk.