Feladat:	B.4702	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	2016/február, 85 - 88. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Térgeometriai bizonyítások, Térelemek és részeik, Kocka
Hivatkozás(ok):	Feladatok: 2015/március: B.4702

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Egy kocka bármely éle a kockának két lapján van rajta és két csúcsát tartalmazza. Mivel kitérő egyenesek nincsenek egy síkban, ezért a kocka minden lapsíkján a három páronként kitérő élegyenes közül pontosan egy van rajta és a kocka nyolc csúcsa közül pontosan kettő olyan van, amelyiken a három páronként kitérő élegyenes közül egyik sem megy át. Feltehető, hogy az $ABCDEFGH$ kocka három páronként kitérő élegyenese közül az egyik a $BC$ (1. ábra). Ekkor a kocka $A$-n, illetve $D$-n átmenő élegyenesei közül csak az egymással párhuzamos $AE$ és $DH$ egyenesek kitérők $BC$-vel. Ezért a három páronként kitérő élegyenes az $ABCD$ lapnak legfeljebb három csúcsát tartalmazza. Ez nyilván a kocka bármely lapjára igaz, ezért minden lapon van legalább egy olyan csúcs, melyet a három páronként kitérő élegyenes egyike sem tartalmaz. De mivel az ilyen csúcsok száma kettő, és minden csúcsra a kockának három lapja illeszkedik, ezért ez azt jelenti, hogy a három páronként kitérő élegyenes által nem tartalmazott két csúcsra a kocka hat lapja közül három-háromnak kell illeszkednie, tehát a két nem tartalmazott csúcs a kocka egy testátlójának két végpontja kell, hogy legyen. 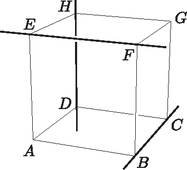  1. ábra   A kockának a $BC$ él felezőmerőleges síkjára való szimmetriája miatt feltehetjük, hogy ez a testátló $AG$. Ekkor a $D$-n átmenő élek közül $DH$ kell, hogy szerepeljen a három páronként kitérő élegyenes közt, s ezért a harmadik egyenes csak $EF$ lehet. Megmutatjuk, hogy az $AG$ testátló minden pontja egyenlő távolságra van a $BC$, $DH$ és $EF$ egyenesektől. Ehhez elegendő belátnunk, hogy a testátló körüli ${120}^{\circ }$-os forgatások a három egyenest ciklikusan permutálják, mert ebből a forgatás szögtartása miatt következik, hogy a testátló egy tetszőleges $T$ pontjából a $BC$, $DH$ és $EF$ egyenesekre bocsájtott merőlegeseket is permutálják a forgatások, azaz $T$ egyenlő távolságra van a három egyenestől. A $BDE$ és $CFH$ háromszögek szabályosak, mert mindegyik oldaluk hossza megegyezik a kocka lapátlójának hosszával. Legyen $K$, illetve $L$ e két szabályos háromszög középpontja. Mivel $AB=AD=AE$ és $GB=GD=GE$, ezért $A$ is és $G$ is rajta van a $BDE$ háromszög síkjára $K$-ban állított merőlegesen, azaz $AG$ merőleges a $BDE$ háromszög síkjára és átmegy $K$-n. Az $AC=AF=AH$ és $GC=GF=GH$ egyenlőségekből pedig ugyanígy az következik, hogy $AG$ merőleges a $CFH$ háromszög síkjára is és átmegy $L$-en is. Ezért az $AG$ körüli ${120}^{\circ }$-os forgatásnál $B$, $D$ és $E$ egy $K$ középpontú körön mozog és $B\mapsto D$, $D\mapsto E$ és $E\mapsto B$, míg $C$, $H$ és $F$ egy $L$ középpontú körön mozog és $C\mapsto H$, $H\mapsto F$ és $F\mapsto C$ (2. ábra). Ez pedig azt jelenti, hogy a három kitérő egyenesre $BC\mapsto DH$, $DH\mapsto EF$ és $EF\mapsto BC$, amit bizonyítani akartunk. 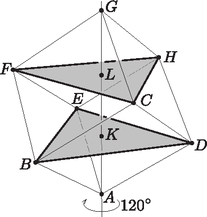  2. ábra 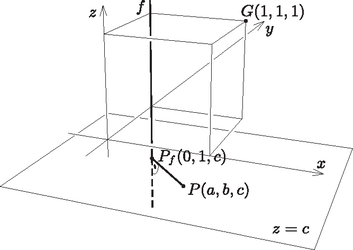    II. megoldás. Vegyünk fel egy térbeli derékszögű koordináta-rendszert úgy, hogy az origója legyen $A$, a tengelyek legyenek párhuzamosak a kocka éleivel és legyen $G=\left(\mathrm{1,1,1}\right)$. Jelöljük a $BC$, $DH$ és $EF$ egyeneseket rendre $e$, $f$ és $g$-vel. Ekkor ezek egyenletrendszere: $\begin{array}{c}{\displaystyle e:X=1\text{ és }Z=0;f:Y=1\text{ és }X=0;g:Z=1\text{ és }Y=0.}\end{array}$   3. ábra   Ha $P=\left(a\mathrm{,}b\mathrm{,}c\right)$ egy tetszőleges pont, akkor a $P$-n átmenő, az $e\mathrm{,}f$ és $g$ egyenesekre merőleges síkok egyenletei rendre 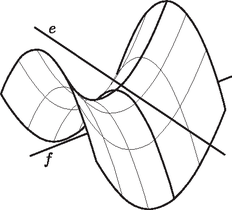$\begin{array}{c}{\displaystyle Y=b\mathrm{,}Z=c\text{és}X=a\mathrm{,}}\end{array}$ e síkoknak az egyenesekkel való metszéspontjai pedig $\begin{array}{c}{\displaystyle P_e=\left(\mathrm{1,}b\mathrm{,0}\right)\mathrm{,}{P}_f=\left(\mathrm{0,1,}c\right)\text{és}{P}_g=\left(a\mathrm{,0,1}\right)\mathrm{.}}\end{array}$ A $P$ pontnak az egyenesektől való távolságai tehát $\begin{array}{c}{\displaystyle P{P}_e=\sqrt[]{{\left(a-1\right)}^2+c^2}\mathrm{,}P{P}_f=\sqrt[]{a^2+{\left(b-1\right)}^2}\text{és}P{P}_g=\sqrt[]{b^2+{\left(c-1\right)}^2}\mathrm{.}}\end{array}$ Látható, hogy ha $a=b=c$, akkor $P{P}_e=P{P}_f=P{P}_g=\sqrt[]{{\left(a-1\right)}^2+a^2}$, tehát a kocka $AG$ testátlójának minden pontja egyenló távolságra van a három páronként kitérő $BC$, $DH$ és $EF$ élegyenestől.   Megjegyzés. A második megoldásból az is látszik, hogy nem csak a testátló pontjai vannak egyenlő távolságra a három élegyenestől. A $P$ pont pontosan akkor van egyenlő távolságra a három egyenestől, ha $P{P}_e=P{P}_f$ és $P{P}_e=P{P}_g$ egyszerre teljesül. Az első egyenlőséget rendezve kapjuk, hogy $\begin{array}{c}{\displaystyle {\left(a-1\right)}^2+c^2=a^2+{\left(b-1\right)}^2\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle c^2-b^2=2\left(a-b\right)\mathrm{.}}\end{array}$ Vagyis $P$ pontosan akkor van egyenlő távolságra az $e$ és $f$ élegyenestől, ha rajta van a $\begin{array}{c}{\displaystyle Z^2-Y^2=2\left(X-Y\right)}\end{array}$ (1) egyenletű felületen. Ez egy jól ismert másodrendű felület, hiperbolikus paraboloidnak, vagy nyeregfelületnek nevezik (4. ábra). Geometriai tulajdonságainak részletes leírása megtalálható pl. Hajós Gy.: Bevezetés a geometriába című könyvének 50.7. fejezetében. Ugyanígy kapjuk, hogy a $P{P}_e=P{P}_g$ feltételnek eleget tevő pontok is egy nyeregfelületen vannak, melynek egyenlete $\begin{array}{c}{\displaystyle X^2-Y^2=2\left(X-Z\right)\mathrm{.}}\end{array}$ (2)   4. ábra   A három éltől egyenlő távolságra lévő pontok pedig a két nyeregfelület közös részén vannak. Két nyeregfelület metszete általában egy negyedrendű térgörbe, esetünkben viszont némileg egyszerűbb a helyzet, mert a metszet szétesik két görbére, melyek egyike az $X=Y=Z$ egyenletrendszerű egyenes. A másik görbét az (1) és (2) egyenletekből álló egyenletrendszer megoldásából kapjuk. Csak két egyenletünk van és három ismeretlen, így egy $t$ paraméter segítségével tudjuk megadni azokat a megoldásokat, melyekre $X\ne Y\ne Z$ teljesül. A számolást most nem részletezzük. A megoldás: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle X\left(t\right)=}& {\displaystyle \frac{t^3-4t+8}{2\left(t^2-2t\right)}\mathrm{,}}\hfill \\ \hfill {\displaystyle Y\left(t\right)=}& {\displaystyle \frac{t^3-4t^2+4t-8}{2\left(t^2-2t\right)}\mathrm{,}}\hfill \\ \hfill {\displaystyle Z\left(t\right)=}& {\displaystyle \frac{-t^3+4t^2-12t+8}{2\left(t^2-2t\right)}\mathrm{.}}\hfill \end{array}}$ Minden $0\ne t\ne 2$ valós számhoz tartozik a metszetgörbének egy pontja. Ha pl. $t=1$, akkor $X\left(t\right)=-5/2$, $Y\left(t\right)=7/2$ és $Z\left(t\right)=1/2$. Tehát az  $\begin{array}{c}{\displaystyle R=\left(-\frac{5}{2}\mathrm{,}\frac{7}{2}\mathrm{,}\frac{1}{2}\right)}\end{array}$ olyan pont, mely mindhárom élegyenestől ugyanolyan távolságra, pontosan $5\sqrt[]{2}/2$-re van.