Feladat:	B.4674	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Baran Zsuzsanna ,  Cseh Kristóf ,  Csépai András ,  Döbröntei Dávid Bence ,  Fekete Panna ,  Gáspár Attila ,  Katona Dániel ,  Kerekes Anna ,  Kocsis Júlia ,  Kovács Márton ,  Kovács Péter Tamás ,  Nagy-György Pál ,  Porupsánszki István ,  Schrettner Bálint ,  Schwarcz Tamás ,  Szebellédi Márton ,  Tóth Viktor ,  Vághy Mihály ,  Varga-Umbrich Eszter ,  Wei Cong Wu ,  Williams Kada
Füzet:	2016/február, 84 - 85. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Mértani helyek, Körülírt kör, Egybevágósági transzformációk
Hivatkozás(ok):	Feladatok: 2014/december: B.4674

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.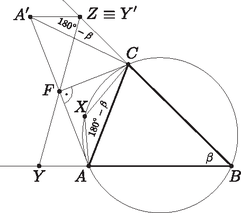   Megoldás. Legyen az $YZ$ szakasz felezőpontja $F$. Jelölje az $A$ és $Y$ pontok $F$-re vonatkozó tükörképét $A\text{'}$ és $Y\text{'}$. Ekkor $Y\text{'}\equiv Z$. Mivel bármely szakasz párhuzamos a középpontos tükörképével, ezért $A\text{'}Z$ párhuzamos $AY$-nal, s így $AB$-vel (1. ábra). Ezért ha az $ABC$ háromszög $B$-nél lévő szöge $\beta$, akkor $A\text{'}ZB\sphericalangle ={180}^{\circ }-\beta$. Az $ABCX$ négyszög húrnégyszög, ezért $AXC\sphericalangle ={180}^{\circ }-ABC\sphericalangle ={180}^{\circ }-\beta$. Tehát az $AXC$ és az $A\text{'}ZC$ háromszögek egybevágóak, mert megegyezik egy szögük és az azt közrefogó két oldaluk, hiszen $AX=AY=A\text{'}Z$ és $CX=CZ$. Vagyis $AC=A\text{'}C$, azaz a $CA\text{'}A$ háromszög egyenlőszárú. Ezért alapjának $F$ felezőpontját a $C$ csúccsal összekötő egyenes az alap felezőmerőlegese, vagyis $CF$ merőleges $FA$-ra. Tehát Thalész tételének megfordítása szerint $F$ rajta van az $AC$ szakasz $k$ Thalész-körén.   1. ábra   Meg kell még vizsgálnunk, hogy $k$ mely pontjai állnak elő az $YZ$ szakaszok felezőpontjaként. Legyen az $ABC$ háromszög $A$-nál, illetve $C$-nél lévő szöge $\alpha$, illetve $\gamma$. Az $X$ pont két szélső helyzete $X_1\equiv A$ és $X_2\equiv C$. Az első esetben $Y_1\equiv A$ és $F_1$ a $C{Z}_{1}A$ egyenlőszárú háromszög $Z_{1}A$ alapjának felezőpontja. Mivel $Z_{1}CA\sphericalangle ={180}^{\circ }-\gamma$, ezért $F_{1}CA\sphericalangle ={90}^{\circ }-\gamma /2$. Ugyanígy kapjuk, hogy ha $X_2\equiv C$, akkor $F_{2}AC\sphericalangle ={90}^{\circ }-\alpha /2$ (2. ábra). Ha $k$ középpontja ($AC$ felezőpontja) $K$, akkor az $F_{1}KC$ és az $F_{2}KA$ egyenlőszárú háromszögekből azt kapjuk, hogy 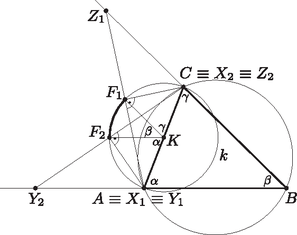$\begin{array}{c}{\displaystyle F_{1}KC\sphericalangle ={180}^{\circ }-2\cdot F_{1}CA\sphericalangle ={180}^{\circ }-2\cdot \left({90}^{\circ }-\frac{\gamma }{2}\right)=\gamma \mathrm{,}}\end{array}$ és ugyanígy $F_{2}KA\sphericalangle =\alpha$, ezért $F_{1}K{F}_2\sphericalangle ={180}^{\circ }-\left(\gamma +\alpha \right)=\beta$.   2. ábra   Ha $X$ folytonosan mozog $A$-ból $C$-be, akkor $F$ is nyilván folytonosan mozog $F_1$-ből $F_2$-be. Tehát a keresett mértani hely az $AC$ szakasz Thalész körének a $\beta$ középponti szögű $F_1{F}_2$ íve.