Feladat:	2015. évi Kürschák matematikaverseny 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Fleiner Tamás
Füzet:	2016/február, 68 - 69. oldal		PDF  |  MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd), Síkgeometriai bizonyítások, Ceva-tétel, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 2016/február: 2015. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.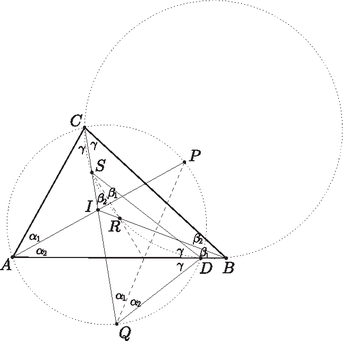   Megoldás. Legyen $\begin{array}{c}{\displaystyle {\alpha }_1=IAC\sphericalangle \mathrm{,}{\alpha }_2=BAI\sphericalangle \mathrm{,}{\beta }_1=IBA\sphericalangle \mathrm{,}{\beta }_2=CBI\sphericalangle \mathrm{,}\gamma =ICB\sphericalangle =ACI\sphericalangle \mathrm{.}}\end{array}$ Írjuk fel a Ceva-tétel trigonometrikus alakját az $ABC$ háromszögre és az $I$ pontra: $\begin{array}{c}{\displaystyle \frac{\text{sin}IAC\sphericalangle }{\text{sin}BAI\sphericalangle }\cdot \frac{\text{sin}IBA\sphericalangle }{\text{sin}CBI\sphericalangle }\cdot \frac{\text{sin}ICB\sphericalangle }{\text{sin}ACI\sphericalangle }=\frac{\text{sin}{\alpha }_1}{\text{sin}{\alpha }_2}\cdot \frac{\text{sin}{\beta }_1}{\text{sin}{\beta }_2}\cdot \frac{\text{sin}\gamma }{\text{sin}\gamma }=1.}\end{array}$     A kerületi szögek tételéből (irányított, azaz modulo ${180}^{\circ }$ szögekkel): ${\displaystyle \begin{array}{cc}\hfill {\displaystyle PQS\sphericalangle }& {\displaystyle =PQC\sphericalangle =PAC\sphericalangle =IAC\sphericalangle ={\alpha }_1\mathrm{,}}\hfill \\ \hfill {\displaystyle DQP\sphericalangle }& {\displaystyle =DAP\sphericalangle =BAI\sphericalangle ={\alpha }_2\mathrm{,}}\hfill \\ \hfill {\displaystyle RSD\sphericalangle }& {\displaystyle =RBD\sphericalangle =IBA\sphericalangle ={\beta }_1\mathrm{,}}\hfill \\ \hfill {\displaystyle QSR\sphericalangle }& {\displaystyle =CSR\sphericalangle =CBR\sphericalangle =CBI\sphericalangle ={\beta }_2\mathrm{,}}\hfill \\ \hfill {\displaystyle ADQ\sphericalangle }& {\displaystyle =ACQ\sphericalangle =ACI\sphericalangle =\gamma \mathrm{,}}\hfill \\ \hfill {\displaystyle SDA\sphericalangle }& {\displaystyle =SDB\sphericalangle =SCB\sphericalangle =ICB\sphericalangle =\gamma \mathrm{.}}\hfill \end{array}}$ Végül alkalmazzuk a Ceva-tétel (trigonometrikus alakjának) megfordítását a  $DSQ$ háromszögre. Mivel $\begin{array}{c}{\displaystyle \frac{\text{sin}ADQ\sphericalangle }{\text{sin}SDA\sphericalangle }\cdot \frac{\text{sin}RSD\sphericalangle }{\text{sin}QSR\sphericalangle }\cdot \frac{\text{sin}PQS\sphericalangle }{\text{sin}DQP\sphericalangle }=\frac{\text{sin}\gamma }{\text{sin}\gamma }\cdot \frac{\text{sin}{\beta }_1}{\text{sin}{\beta }_2}\cdot \frac{\text{sin}{\alpha }_1}{\text{sin}{\alpha }_2}=\mathrm{1,}}\end{array}$ a $DA=AB$, $RS$ és $PQ$ egyenesek egy ponton mennek át, vagy párhuzamosak egymással. $\square$   Megjegyzés. Láttuk, hogy az $ABC$ háromszög hasonló a $QSD$ háromszöghöz. Legyen $I\text{'}$ az $ABC$ háromszög $I$ pontjának megfelelője a $QSD$ háromszögben. A fenti bizonyítás kulcsa az, hogy a $QSD$ háromszögben az $I\text{'}$ izogonális konjugáltja éppen az $AB$, $PQ$ és $RS$ egyenesek közös pontja.