Feladat:	2015. évi Eötvös fizikaverseny 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2016/január, 50 - 53. oldal		PDF  |  MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén), Nyugalmi indukció
Hivatkozás(ok):	Feladatok: 2016/január: 2015. évi Eötvös fizikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A hosszú tekercsben folyó áram hatására a tekercs belsejében valamekkora, időben periodikusan változó $\Phi \left(t\right)$ mágneses fluxus jön létre. A változó mágneses fluxus a hosszú tekercs minden menetében feszültséget indukál, ezek összege minden pillanatban megegyezik a tekercsre kapcsolt váltakozó feszültséggel: $\begin{array}{c}{\displaystyle U_1\left(t\right)=N_1\frac{\Delta \Phi \left(t\right)}{\Delta t}\mathrm{.}}\end{array}$ A lapos tekercsben nem folyik áram (a voltmérő ellenállása nagyon nagy), de a hosszú tekercs szórt mágneses tere feszültséget indukál benne. A feladat ennek a szórt térnek a meghatározása. A tekercsen kívüli mágneses mező ($D_1\ll \ell$ miatt) jó közelítéssel olyan, mintha a tekercs egyik végén egy pontszerű forrásból összesen $\Phi \left(t\right)$ mágneses fluxus indulna ki gömbszimmetrikusan, a tekercs másik végén pedig ugyanekkora fluxus nyelődne el (vagyis mintha egy $-\Phi \left(t\right)$ erősségű forrás helyezkedne el ott). A lapos tekercs a hosszú tekercs felezősíkjában, a hosszú tekercshez közel helyezkedik el, így ezen a helyen mindkét forrás külön-külön $\begin{array}{c}{\displaystyle B\left(t\right)=\frac{\Phi \left(t\right)}{4\pi {\left(\frac{\ell }{2}\right)}^2}}\end{array}$ mágneses indukciót hoz létre (mert a $\Phi$ fluxus egy $\ell /2$ sugarú gömb felületén oszlik el egyenletesen). A lapos tekercs közel van a hosszú tekercshez, így $B$ közel merőleges a felületére. A lapos tekercsen áthaladó teljes (mindkét forrásból származó) fluxus emiatt: $\begin{array}{c}{\displaystyle {\Phi }_2\left(t\right)=2B\left(t\right)\pi {\left(\frac{D_2}{2}\right)}^{}2=\frac{1}{2}{\left(\frac{D_2}{\ell }\right)}^2\Phi \left(t\right)\mathrm{.}}\end{array}$ Ez az időben változó fluxus a lapos tekercsben $\begin{array}{c}{\displaystyle U_2\left(t\right)=N_2\frac{\Delta {\Phi }_2\left(t\right)}{\Delta t}=\frac{1}{2}{N}_2{\left(\frac{D_2}{\ell }\right)}^2\frac{\Delta \Phi \left(t\right)}{\Delta t}=\frac{1}{2}\frac{N_2}{N_1}{\left(\frac{D_2}{\ell }\right)}^2{U}_1\left(t\right)}\end{array}$ feszültséget indukál. (Felhasználtuk $U_1\left(t\right)$ korábban felírt kifejezését.) Az $U_1\left(t\right)$ és $U_2\left(t\right)$ feszültségek minden pillanatban arányosak egymással, így az effektív értékek aránya is ugyanekkora. Ebből a keresett feszültség: $\begin{array}{c}{\displaystyle U_2=\frac{1}{2}\frac{N_2}{N_1}{\left(\frac{D_2}{\ell }\right)}^2{U}_1\approx 4\mathrm{,}5\text{mV}\mathrm{.}}\end{array}$   II. megoldás (Fehér Zsombor megoldása alapján). Egy hosszú, egyenes tekercs (szolenoid) belsejében kialakuló mágneses indukció nagyságára jól ismert a következő összefüggés: $\begin{array}{c}{\displaystyle B_0={\mu }_0\frac{N_{1}I}{\ell }\mathrm{,}}\end{array}$ ahol $N_1$ a tekercs menetszáma, $I$ a tekercsen átfolyó áramerősség, $\ell$ a tekercs hossza és ${\mu }_0=4\pi \cdot {10}^{-7}\text{Vs/(Am)}$. Ez az összefüggés azonban véges hosszúságú tekercsre csak közelítőleg igaz! A véges hosszúságú tekercs terét a tekercs középpontjában helyesen a következő kifejezés adja meg: $\begin{array}{c}{\displaystyle B_{\text{bent}}=B_0\text{cos}\alpha ={\mu }_0\frac{N_{1}I}{\ell }\text{cos}\alpha \mathrm{,}}\end{array}$ ahol $\alpha$ a tekercs zárókörének fél látószöge a középpontból nézve (9. ábra). Ez az összefüggés a Biot‐Savart-törvény segítségével (integrálszámítással, de akár elemi eszközökkel is) levezethető (lásd lentebb a 2. megjegyzést).   9. ábra   Hosszú, vékony tekercsnél $\begin{array}{c}{\displaystyle \alpha \approx \text{tg}\alpha =\frac{D_1}{\ell }\ll \mathrm{1,}}\end{array}$ és így $\text{cos}\alpha \approx 1$, tehát az ismert összefüggés általában jó közelítésként használható. Ebben a feladatban azonban ‐ mint látni fogjuk ‐ éppen ennek a közelítésnek a pontossága, vagyis $B_0$ és $B_{\text{bent}}$ kicsiny különbsége lesz számunkra fontos! Írjuk fel a gerjesztési törvényt egy olyan kis téglalapra, amelynek két oldala a két tekercs tengelyén fekszik (10. ábra): $\begin{array}{c}{\displaystyle B_{\text{bent}}\Delta \ell +B_{\text{kint}}\Delta \ell ={\mu }_0\frac{N_{1}I}{\ell }\Delta \ell \left(=B_0\Delta \ell \right)\mathrm{,}}\end{array}$ ahol $B_{\text{kint}}$ a rövid tekercsben lévő mágneses indukció nagysága, $N_{1}I\frac{\Delta \ell }{\ell }$ pedig a nagy tekercs azon meneteinek száma, amelyeket a kis hurok körülfog. (Felhasználtuk, hogy a tengelyre merőleges indukciókomponens a szolenoid tengelye tájékán elhanyagolható.) Innen következik, hogy 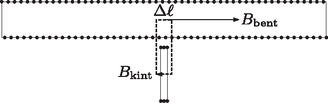$\begin{array}{c}{\displaystyle B_{\text{kint}}=B_0-B_{\text{bent}}=B_0\left(1-\text{cos}\alpha \right)=B_0\cdot 2\text{sin}{}^2\frac{\alpha }{2}\approx B_{\text{bent}}\frac{1}{2}{\left(\frac{D_1}{\ell }\right)}^2\mathrm{.}}\end{array}$   10. ábra   A tekercsekben indukált feszültség arányos a tekercsek menetszámával és az egy meneten áthaladó fluxussal, amiből a keresett feszültség: $\begin{array}{c}{\displaystyle U_2=\frac{N_2{B}_{\text{kint}}\pi {\left(\frac{D_2}{2}\right)}^2}{N_1{B}_{\text{bent}}\pi {\left(\frac{D_1}{2}\right)}^2}{U}_1=\frac{1}{2}\frac{N_2}{N_1}{\left(\frac{D_2}{\ell }\right)}^2{U}_1\mathrm{,}}\end{array}$ az I. megoldással megegyezően.   Megjegyzések. 1. A megoldásban nem használtuk fel a megadott adatok közül a hosszú tekercs $D_1$ átmérőjének és a frekvenciának a számértékét. Ugyanakkor mindkét adat nagyságrendje fontos a megoldáshoz! Felhasználtuk, hogy $D_1\ll \ell$, mert emiatt közelíthettük a külső teret két pontforrás terével. A hosszú tekercs induktív ellenállása, és így a tekercsen folyó áram nagysága függ a frekvenciától. Ha a frekvencia sokkal kisebb (például $50\text{Hz}$) lenne, akkor a tekercsen a rákapcsolt $100\text{V}$ feszültség hatására olyan nagy áram indulna meg, amely a tekercset azonnal szétolvasztaná. 2. A véges hosszúságú tekercs terének levezetése. Egy $r$ sugarú körvezetőben folyó $\Delta I$ erősségű áram által keltett mágneses indukciót a kör síkjára merőleges szimmetriatengely pontjaiban könnyen kiszámíthatjuk a Biot‐Savart-törvény segítségével. A szimmetriatengely azon pontjában, ahonnan a körvezető sugara $\phi$ szögben látszik, tehát amely ponttól a körvezető pontjai $R=r/\text{sin}\phi$ távol vannak (11. ábra), a mágneses indukció 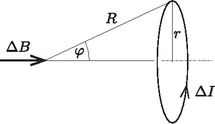$\begin{array}{c}{\displaystyle \Delta B={\mu }_0\frac{\Delta I}{4\pi }\frac{2r\pi }{R^2}\text{sin}\phi ={\mu }_0\frac{\Delta I}{2r}\text{sin}{}^3\phi \mathrm{.}}\end{array}$   11. ábra   Rakjuk össze az $\ell$ hosszúságú $N$ menetes tekercset $\Delta \ell$ vastagságú kis köráramokból. Ekkor egy ilyen kis körben $\begin{array}{c}{\displaystyle \Delta I=\frac{NI}{\ell }\Delta \ell }\end{array}$ áram folyik, ami a tengelye mentén, a $\phi$ szöggel jellemezhető pontban $\begin{array}{c}{\displaystyle \Delta B={\mu }_0\frac{NI}{2r\ell }\text{sin}{}^3\phi \Delta \ell }\end{array}$ indukciót hoz létre. 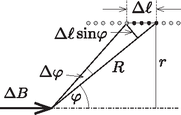  12. ábra   Kihasználva, hogy a tekercs alkotójának kicsiny $\Delta \ell$ hosszúságú darabja a kérdéses pontból $\begin{array}{c}{\displaystyle \Delta \phi \approx \frac{\Delta \ell \cdot \text{sin}\phi }{R}=\frac{\text{sin}{}^2\phi }{r}\cdot \Delta \ell }\end{array}$ szög alatt látszik (12. ábra), a körvezetők mágneses indukciója így is felírható: $\begin{array}{c}{\displaystyle \Delta B={\mu }_0\frac{NI}{2\ell }\text{sin}\phi \Delta \phi \mathrm{.}}\end{array}$ A tekercs középpontjában létrejövő mágneses indukciót úgy kapjuk meg, hogy ezeket a kis indukciójárulékokat összegezzük $\phi =\alpha$-től $\phi =\pi -\alpha$-ig ($\alpha$ a tekercs zárókörének fél látószöge a tekercs középpontjából). $\begin{array}{c}{\displaystyle B=\sum _{\phi =\alpha }^{\pi -\alpha }\Delta B={\mu }_0\frac{NI}{2\ell }\sum _{\phi =\alpha }^{\pi -\alpha }\text{sin}\phi \Delta \phi \mathrm{.}}\end{array}$ A fenti képlet végén szereplő összeget egyszerű fizikai megfontolásokkal is meghatározhatjuk. Ha egy $m$ tömegű gyöngyszemet egy függőleges síkban rögzített $r$ rugarú körív mentén (mindvégig érintő irányú erőt alkalmazva) lassan felemeljük a 13. ábrán látható $P_1$ pontból a $P_2$ pontig, akkor a végzett munka $\begin{array}{c}{\displaystyle W=\sum F\left(\phi \right)\Delta s=mgr\sum _{\phi =\alpha }^{\pi -\alpha }\text{sin}\phi \Delta \phi \mathrm{.}}\end{array}$ Másrészt ez a munka a gyöngyszem helyzeti energiájának megváltozásával egyenlő: $\begin{array}{c}{\displaystyle W=2mgr\text{cos}\alpha \mathrm{,}}\end{array}$ tehát $\begin{array}{c}{\displaystyle \sum _{\phi =\alpha }^{\pi -\alpha }\text{sin}\phi \Delta \phi =2\text{cos}\alpha \mathrm{.}}\end{array}$ Ennek ismeretében a véges hosszúságú tekercs mágneses indukciója a tekercs közepénél: 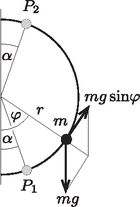$\begin{array}{c}{\displaystyle B={\mu }_0\frac{NI}{\ell }\cdot \text{cos}\alpha \mathrm{.}}\end{array}$   13. ábra