Feladat:	2015. évi Eötvös fizikaverseny 1. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	2016/január, 45 - 47. oldal		PDF  |  MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén), Egyenesvonalú mozgás lejtőn
Hivatkozás(ok):	Feladatok: 2016/január: 2015. évi Eötvös fizikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.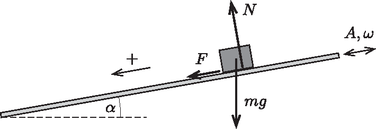   Megoldás. Az $m$ tömegű hasábra az $mg$ nehézségi erő, az $N$ kényszererő és az $F$ (csúszási vagy tapadási) súrlódási erő hat (utóbbi iránya a deszkalap rezgetése során változik). A test mozgásegyenletei a lejtőre merőleges, illetve azzal párhuzamos irányban: $\begin{array}{c}{\displaystyle N-mg\text{cos}\alpha =\mathrm{0,}F+mg\text{sin}\alpha =ma\mathrm{.}}\end{array}$ A gyorsulásnál a lejtés irányát választottuk pozitívnak, lásd a 2. ábrát.   2. ábra   Tapadás esetén a kényszererő és a súrlódási erő között az $|F|\le \mu N$ egyenlőtlenség áll fenn, míg csúszásnál $|F|=\mu N$. A hasáb gyorsulása akkor a lehető legnagyobb, ha a hasáb csúszik, és a hasáb deszkához viszonyított (relatív) sebessége negatív irányba mutat. Ekkor $\begin{array}{c}{\displaystyle a_{\text{<span style="font-weight: normal;font-style: normal;">max</span>}}=g\left(\text{sin}\alpha +\mu \text{cos}\alpha \right)\mathrm{,}}\end{array}$ amelyre az adatok behelyettesítése után $a_{\text{<span style="font-weight: normal;font-style: normal;">max</span>}}\approx 5\mathrm{,}6\text{m}{\text{s}}^{-2}$ adódik. A deszkalap legnagyobb gyorsulása a harmonikus rezgés következtében $A{\omega }^2=250\text{<span style="font-weight: normal;font-style: normal;">m</span>}{\text{s}}^{-2}$, amely több mint 40-szer akkora, mint $a_{\text{<span style="font-weight: normal;font-style: normal;">max</span>}}$ értéke, így a hasáb a rezgetés indításakor azonnal megcsúszik. Látni fogjuk, hogy a test a további mozgása során sehol sem tapad meg, tehát mindvégig az (állandó nagyságú) csúszási súrlódási erő hat rá. A hasáb gyorsulása a mozgás során tehát kétféle értéket vehet fel aszerint, hogy a súrlódási erő éppen a pozitív vagy negatív irányba mutat: $\begin{array}{c}{\displaystyle a_{\pm }=g\left(\text{sin}\alpha \pm \mu \text{cos}\alpha \right)\mathrm{,}}\end{array}$ (1) és mivel a megadott számadatok szerint $\mu >\text{tg}\alpha$, így $a_{+}$ előjele pozitív, $a_{-}$ előjele pedig negatív. Az $a_{+}$ gyorsulású mozgásszakasz addig tart, amíg a deszka (előjeles) sebessége nagyobb a hasáb sebességénél, míg az $a_{-}$ gyorsulású mozgásszakaszban a helyzet éppen fordított. A 3. ábrán látható grafikonon ábrázoltuk a deszkalap és a hasáb sebességét az idő függvényében. Utóbbi egy olyan töröttvonallal ábrázolható, ahol az egyes szakaszok meredeksége $a_{+}$ és $a_{-}$. Mivel $|a_{+}|>|a_{-}|$, így a hasáb egy periódusra vett átlagsebessége (a ,,sodródási sebesség'') egyre növekszik, miközben a test lefelé sodródik a deszkán.   3. ábra   A sodródási sebesség növekedése addig tart, amíg a hasáb átlaggyorsulása zérussá nem válik. Ezután a hasáb sebessége egy állandó $v_{\text{<span style="font-weight: normal;font-style: normal;">drift</span>}}$ érték körül fluktuál (4. ábra). Ez az állandósult (stacionárius) mozgás a viszonylag nagy rezgetési frekvencia miatt hamar kialakul, így a teljes mozgási idő becslésekor a kezdeti felgyorsulás időszakát el is hanyagolhatjuk. 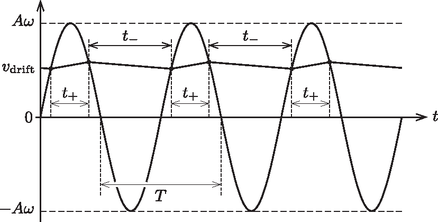  4. ábra   Az állandósult sodródás feltétele: $\begin{array}{c}{\displaystyle \langle a\rangle \equiv \frac{a_{+}{t}_{+}+a_{-}{t}_{-}}{T}=0.}\end{array}$ (2) Természetesen fennáll a $\begin{array}{c}{\displaystyle T=t_{+}+t_{-}}\end{array}$ (3) egyenlőség is. Az $\left(1\right)$-$\left(3\right)$ egyenletekből megkaphatjuk a $t_{+}$ időtartam hosszát: $\begin{array}{c}{\displaystyle t_{+}=\frac{a_{-}}{a_{-}-a_{+}}T=\left(1-\frac{\text{tg}\alpha }{\mu }\right)\frac{T}{2}\mathrm{.}}\end{array}$ (4) A sodródási sebességet pedig abból a feltételből határozhatjuk meg, hogy a hasáb gyorsulása akkor vált irányt, amikor a deszka és a hasáb sebessége megegyezik. A sebesség ($v_{\text{<span style="font-weight: normal;font-style: normal;">drift</span>}}$ értékéhez képest kicsiny) fluktuációját elhanyagolva: $\begin{array}{c}{\displaystyle v_{\text{<span style="font-weight: normal;font-style: normal;">drift</span>}}\approx A\omega \text{cos}\left(\omega \frac{t_{+}}{2}\right)\mathrm{.}}\end{array}$ Végül, behelyettesítve a $\left(4\right)$ eredményt: $\begin{array}{c}{\displaystyle v_{\text{<span style="font-weight: normal;font-style: normal;">drift</span>}}=A\omega \text{cos}\left[\left(1-\frac{\text{tg}\alpha }{\mu }\right)\frac{\pi }{2}\right]=A\omega \text{sin}\left(\frac{\pi \text{tg}\alpha }{2\mu }\right)\mathrm{.}}\end{array}$ A számszerű adatokat felhasználva $v_{\text{<span style="font-weight: normal;font-style: normal;">drift</span>}}\approx 0\mathrm{,}32\text{<span style="font-weight: normal;font-style: normal;">m</span>}{\text{s}}^{-1}$ értéket kapunk, így a hasáb mozgásának becsült ideje $\begin{array}{c}{\displaystyle t=\frac{L}{v_{\text{<span style="font-weight: normal;font-style: normal;">drift</span>}}}\approx 18\mathrm{,}8\text{<span style="font-weight: normal;font-style: normal;">s</span>}\mathrm{.}}\end{array}$ Hátravan még annak belátása, hogy a hasáb valóban nem tapad meg soha a lejtőn. A megtapadásnak két feltétele van: az egyik, hogy egy adott pillanatban a test és a deszkalap sebessége megegyezzen; a másik, hogy ugyanebben a pillanatban a deszka gyorsulásának nagysága kisebb legyen $|a_{+}|$-nál vagy $|a_{-}|$-nál aszerint, hogy a deszka épp lefelé vagy felfelé gyorsul. A sebesség-idő grafikonról látszik, hogy ez a két feltétel csak akkor következhet be, amikor a deszka gyorsulása nagyon kicsi, azaz sebessége nagy ($A\omega$-hoz közeli). Ekkora sebességre azonban nem tud felgyorsulni a hasáb, mert már előbb beáll a nála jóval kisebb $v_{\text{<span style="font-weight: normal;font-style: normal;">drift</span>}}$. A hasáb tehát végig csúszva halad a lejtőn.   Megjegyzés. A megoldás során felhasználtuk, hogy a mozgás első, átmeneti szakasza (amely alatt a hasáb átlagsebessége eléri a $v_{\text{<span style="font-weight: normal;font-style: normal;">drift</span>}}$ értéket) rövid. Részletesebb számolással megmutatható, hogy ez az időtartam $\begin{array}{c}{\displaystyle \tau \approx \frac{A\omega }{\mu g\text{cos}\alpha }\approx 0\mathrm{,}13\text{<span style="font-weight: normal;font-style: normal;">s</span>}}\end{array}$ nagyságrendű, tehát a becslésnél elkövetett hibánk valóban elhanyagolható (1‐2% körüli érték).