Feladat:	B.4714	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Nagy Dávid Paszkál
Füzet:	2016/január, 27. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Kombinatorikus geometria, Indirekt bizonyítási mód
Hivatkozás(ok):	Feladatok: 2015/május: B.4714

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. A 2015 pont akkor alkot konvex $2015$-szöget, ha közülük semelyik 3 nem esik egy egyenesbe és mindegyikük rajta van a konvex burkuk határán. Az adott pontok közül semelyik három nem eshet egy egyenesbe, mert akkor a három kollineáris ponthoz egy tetszőleges negyediket választva négy olyan pontot kapnánk, amik nem alkotnak konvex négyszöget. Tegyük fel, hogy a pontok nem egy konvex $2015$-szög csúcsai. Mivel a pontok nem esnek egy egyenesre, ezért ekkor konvex burkuk, $\text{K}$, egy konvex $n$-szög valamely $n<2015$ egészre, továbbá a pontok közül legalább egy $\text{K}$ belsejébe esik. Válasszuk ki $\text{K}$ egyik csúcsát (az ábrán $A_1$), és húzzuk be az ebből kiinduló $n-3$ darab átlót. Ezek $\text{K}$-t $n-2$ darab háromszögre osztják, s e háromszögek teljesen lefedik $\text{K}$-t. Ezért ha $P$ olyan pont a $2015$ közül, mely $\text{K}$ belsejébe esik, akkor az átlók által meghatározott $n-2$ háromszög között van egy olyan (az ábrán $A_1{A}_i{A}_{i+1}$), amelyiknek a belsejébe esik. Ekkor viszont $P$ és az azt tartalmazó háromszög három csúcsa nem alkot konvex négyszöget. Ez az ellentmondás bizonyítja állításunkat.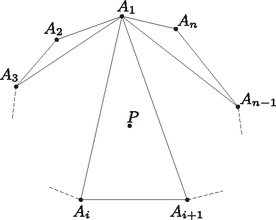