Feladat:	B.4697	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Somogyi Pál
Füzet:	2016/január, 24. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Trapézok, Párhuzamos szelőszakaszok tétele
Hivatkozás(ok):	Feladatok: 2015/március: B.4697

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.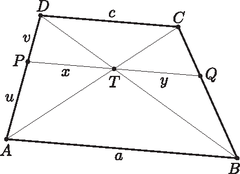   Megoldás. Először megmutatjuk, hogy tetszőleges trapézban az átlók metszéspontján áthaladó, az alapokkal párhuzamos egyenesnek a trapézba eső szakasza a két alap hosszának harmonikus közepével megegyező hosszúságú.     $PT\parallel AB$, ezért a szelőszakaszok tételéből az 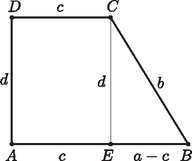$ABD$ háromszögben $\begin{array}{c}{\displaystyle \frac{x}{a}=\frac{v}{u+v}\mathrm{,}}\end{array}$ az $ACD$ háromszögből pedig hasonlóan $\begin{array}{c}{\displaystyle \frac{x}{c}=\frac{u}{u+v}\mathrm{.}}\end{array}$ A két egyenlőséget összeadva: $\begin{array}{c}{\displaystyle \frac{x}{a}+\frac{x}{c}=\frac{v}{u+v}+\frac{u}{u+v}=1.}\end{array}$ Innen pedig rendezéssel: $\begin{array}{c}{\displaystyle x=\frac{ac}{a+c}\mathrm{.}}\end{array}$ Az $ABC$ háromszögben a $QT$ szakaszra ugyanezekkel a lépésekkel szintén azt kapjuk, hogy $\begin{array}{c}{\displaystyle y=\frac{ac}{a+c}\mathrm{.}}\end{array}$ Tehát $\begin{array}{c}{\displaystyle PQ=x+y=\frac{2ac}{a+c}\mathrm{.}}\end{array}$     Térjünk rá a feladatban szereplő trapézra. Felhasználjuk Pitagorasz tételét és azt az ismert tényt, hogy érintőnégyszög szemközti oldalainak összege egyenlő: $a+c=b+d$, vagyis $b=a+c-d$. Az eddigieket felhasználva írjuk fel a $BEC$ derékszögű háromszögre a Pitagorasz-tételt: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle d^2+{\left(a-c\right)}^2}& {\displaystyle =b^2={\left(a+c-d\right)}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle d^2+a^2-2ac+c^2}& {\displaystyle =a^2+c^2+d^2+2ac-2cd-2ad\mathrm{.}}\hfill \end{array}}$ Egyszerűsítések és rendezés után $\begin{array}{c}{\displaystyle ad+cd=2ac\mathrm{,}d=\frac{2ac}{a+c}\mathrm{.}}\end{array}$ A két számítást összevetve beláttuk, hogy $PQ=AD$.