Feladat:	B.4665	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Andó Angelika ,  Baglyas Márton ,  Balogh Menyhért ,  Borbényi Márton ,  Erdei Ákos ,  Fehér Balázs ,  Gál Boglárka ,  Hegyi Zoltán ,  Horváth Péter ,  Kasó Ferenc ,  Kerekes Anna ,  Kovács Péter Tamás ,  Kovács Viktória ,  Lakatos Ádám ,  Nagy-György Zoltán ,  Pálfi Mária ,  Polgár Márton ,  Széles Katalin ,  Urbán Miklós Vlagyimír ,  Vághy Mihály ,  Varga-Umbrich Eszter ,  Wiandt Péter
Füzet:	2015/május, 282 - 286. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Paraméteres egyenletek, Parabola egyenlete
Hivatkozás(ok):	Feladatok: 2014/november: B.4665

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A feladatot grafikusan oldjuk meg. Derékszögű koordinátarendszerben ábrázoljuk az $Y=mX+4$ és az $Y=|X^2-10X+21|$ függvényeket. A két görbe közös pontjainak a száma adja az eredeti egyenlet megoldásainak számát. Az $Y=mX+4$ egy egyenes egyenlete. Jelöljük ezt az egyenest $e_m$-mel. Ha $X=0$, akkor $Y=4$, ezért $e_m$ mindig átmegy a koordinátarendszer $A=\left(0;4\right)$ pontján. Az egyenes meredeksége az $m$ értékétől függ, s tekinthetjük úgy, hogy ha $m$-et változtatjuk, akkor $e_m$ az $A$ körül forog. Az $Y=X^2-10X+21$ függvény képe egy olyan felfelé nyíló $\text{P}$ parabola, mely a $B=\left(3;0\right)$ és a $C=\left(7;0\right)$ pontokban metszi az $x$ tengelyt (mert az $x^2-10x+21=0$ egyenlet gyökei $3$ és $7$). Ezért az $Y=|X^2-10X+21|$ függvény $\text{G}$ képét úgy kapjuk, hogy $x\le 3$, valamint $7\le x$ esetén tekintjük $\text{P}$ megfelelő íveit, ha pedig $3<x<7$, akkor $\text{P}$-nek az $x$-tengelyre vonatkozó $\text{P}\text{'}$ tükörképét, ami éppen az $Y=-\left(X^2-10X+21\right)$ egyenletű parabola megfelelő íve (1. ábra). Azt kell tehát meghatároznunk, hogy az $e_m$ egyenesnek hány közös pontja van a két parabola darabjaiból összerakott görbével. 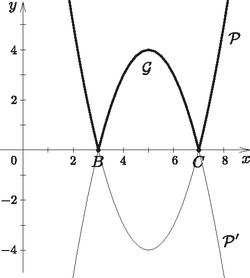  1. ábra   Tudjuk, hogy egy külső $K$ pontból egy parabolához két érintő húzható (lásd pl. Kiss Gy.: Amit jó tudni a kúpszeletekről I. és II., KöMaL 54 (2004), 450‐459. és 514‐518. o.; http://www.komal.hu/cikkek/2004-11/kupszeletek1.h.shtml). Ha a koordinátarendszerben egy parabola tengelye függőleges, akkor a $K$-n átmenő egyenesek közül a függőlegesnek egy közös pontja van a parabolával, ha pedig a $K$-ból a parabolához húzott érintők meredeksége $t_1<t_2$, akkor a $K$-n átmenő $m$ meredekségű egyeneseknek $t_1<m<t_2$ esetén nincs, $m<t_1$ és $t_2<m$ esetén pedig pontosan két közös pontjuk van a parabolával (2. ábra). 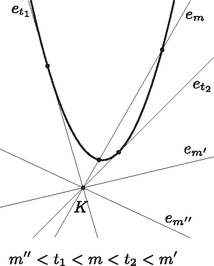  2. ábra   Határozzuk meg az $A$-ból $\text{P}$-hez húzható érintők meredekségét. Az $e_m$ egyenes akkor érintő, ha az $\begin{array}{c}{\displaystyle mx+4=x^2-10x+\mathrm{21,}\text{azaz}{x}^2-\left(10+m\right)x+17=0}\end{array}$ egyenletnek egy megoldása van. Ez pontosan akkor teljesül, ha az egyenlet diszkriminánsa $0$, vagyis ha ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(10+m\right)}^2-4\cdot 17=\mathrm{0,}\text{azaz}}\hfill \\ \hfill {\displaystyle m^2+20m+32=\mathrm{0,}}\hfill \end{array}}$ amiből kapjuk, hogy $m_{\mathrm{1,2}}=-10\pm \sqrt[]{68}$. Ugyanígy kapjuk, hogy az $A$-ból $\text{P}\text{'}$-höz húzható érintők meredeksége $m_3=0$ és $m_4=20$. A metszéspontok számának meghatározásához még szükségünk van az $AB$ és $AC$ egyenesek meredekségére, ami a pontok koordinátáiból könnyen adódik, $AB$ esetén $m_5=\left(0-4\right)/\left(3-0\right)=-4/3$, $AC$ esetén pedig $m_6=\lef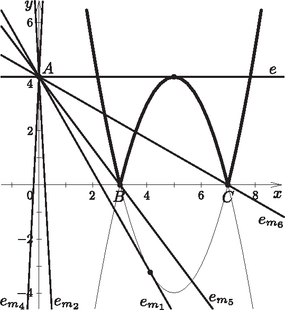t(0-4\right)/\left(7-0\right)=-4/7$ (3. ábra).   3. ábra   Ezek után az $mX+4=|X^2-10X+21|$ egyenlet megoldásainak számát leolvashatjuk a 3. ábráról. $•$ Ha $m<-10-\sqrt[]{68}$, akkor $2$ megoldás van, mert $e_m$ két-két pontban metszi $\text{P}$-t is és $\text{P}\text{'}$-t is, de a négy metszéspont közül csak kettő tartozik $\text{G}$-hez, mert a $\text{P}\text{'}$-vel vett metszéspontok az $x$ tengely alatt vannak. $•$ Ha $m=-10-\sqrt[]{68}$, akkor $1$ megoldás van, mert $e_m$ érinti $\text{P}$-t és két pontban metszi $\text{P}\text{'}$-t, de e két utóbbi pont nem tartozik $\text{G}$-hez, mert az $x$ tengely alatt vannak. $•$ Ha $-10-\sqrt[]{68}<m<-4/3$, akkor a megoldások száma $0$, mert $e_m$ és $\text{P}$ valamennyi (nulla, egy, vagy kettő) metszéspontja, továbbá $e_m$ és $\text{P}\text{'}$ két metszéspontja is az $x$ tengely alatt van, ezért nem tartozik $\text{G}$-hez. $•$ Ha $m=-4/3$, akkor $1$ megoldás van, mert $e_m$ két-két pontban metszi $\text{P}$-t is és $\text{P}\text{'}$-t is, de a négy metszéspont közül kettő egybeesik $B$-vel, a másik kettő pedig nem tartozik $\text{G}$-hez, mert az $x$ tengely alatt van. $•$ Ha $-4/3<m<-4/7$, akkor $2$ megoldás van, mert $e_m$ két-két pontban metszi $\text{P}$-t is és $\text{P}\text{'}$-t is, de a metszéspontok közül csak egy-egy tartozik $\text{G}$-hez, mert a másik két pont az $x$ tengely alatt van. $•$ Ha $m=-4/7$, akkor $3$ megoldás van, mert $e_m$ két-két $\text{G}$-hez tartozó pontban metszi $\text{P}$-t is és $\text{P}\text{'}$-t is, de a négy metszéspont közül kettő egybeesik $C$-vel. $•$ Ha $-4/7<m<0$, akkor $4$ megoldás van, mert $e_m$ két-két pontban metszi $\text{P}$-t is és $\text{P}\text{'}$-t is, és a metszéspontok mindegyike $\text{G}$-hez tartozik. $•$ Ha $m=0$, akkor $3$ megoldás van, mert $e_m$ két pontban metszi $\text{P}$-t és érinti $\text{P}\text{'}$-t, és a közös pontok mindegyike $\text{G}$-hez tartozik. $•$ Ha $0<m$, akkor $2$ megoldás van, mert $e_m$ két $\text{G}$-hez tartozó pontban metszi $\text{P}$-t, a $\text{P}\text{'}$-vel közös pontjai (nulla, egy vagy kettő, attól függően, hogy $m<20$, $m=20$ vagy $m>20$) pedig az $x$ tengely alatt vannak, ezért nem tartoznak $\text{G}$-hez.   II. megoldás. Az abszolútérték definiciója szerint $X^2-10X+21\ge 0$ esetén az $mX+4=X^2-10X+21$, míg $X^2-10X+21<0$ esetén az $mX+4=-\left(X^2-10X+21\right)$ egyenletet kell megoldanunk.   1. eset. Ha $X^2-10X+21\ge 0$, akkor $X\ge 7$ vagy $X\le 3$. Vizsgáljuk meg, hogy az $X^2-\left(m+10\right)X+17=0$ egyenlet megoldásai milyen $m$ értékek esetén esnek a megadott tartományokba. A megoldóképlet alapján a gyökök $\begin{array}{c}{\displaystyle X_1=\frac{m+10+\sqrt[]{m^2+20m+32}}{2}\text{és}{X}_2=\frac{m+10-\sqrt[]{m^2+20m+32}}{2}\mathrm{.}}\end{array}$ Tehát csak akkor vannak valós gyökök, ha $m^2+20m+32\ge 0$, azaz ha $m\le -10-\sqrt[]{68}$ vagy $-10+\sqrt[]{68}\le m$ teljesül. Ha $X_1\ge 7$, akkor ezt átrendezve kapjuk, hogy $\sqrt[]{m^2+20m+32}\ge 4-m$. Ha $4-m\ge 0$, akkor a négyzetreemelés ekvivalens átalakítás. Rendezés után $m\ge -\frac{4}{7}$ következik. Összevonva a feltétellel: $4\ge m\ge -\frac{4}{7}$. Ha $m>4$, akkor a diszkrimináns nemnegatív, $4-m<0$, tehát az egyenlőtlenség teljesül. Vagyis összegezve: $m\ge -\frac{4}{7}$. Ha $X_1\le 3$, akkor ezt átrendezve kapjuk, hogy $\sqrt[]{m^2+20m+32}\le -4-m$, ami csak akkor teljesülhet, ha $-4\ge m$. Továbbá a $m^2+20m+32\ge 0$ egyenlőtlenségnek is fenn kell állnia, ezért $m\le -10-\sqrt[]{68}$. Ekkor négyzetreemelés és rendezés után kapjuk, hogy $m\le -4/3$, tehát az $X_1\le 3$ egyenlőtlenség pontosan akkor teljesül, ha $m\le -10-\sqrt[]{68}$. Ha $X_2\ge 7$, akkor ezt átrendezve kapjuk, hogy $m-4\ge \sqrt[]{m^2+20m+32}$, amiből négyzetreemelés és újabb rendezés után $m\le -4/7$ következik. Ha ez teljesül, akkor $m-4<0$, ezért a négyzetreemelés nem volt ekvivalens átalakítás, az eredeti egyenlőtlenség nem áll fenn. Tehát $X_2\ge 7$ soha nem teljesül. Ha $X_2\le 3$, akkor ezt átrendezve kapjuk, hogy $m+4\le \sqrt[]{m^2+20m+32}$. Ez $m\le -10-\sqrt[]{68}$ esetén nyilván teljesül, ha pedig $-10+\sqrt[]{68}\le m$, akkor négyzetreemelés és rendezés után kapjuk, hogy $m\ge -4/3$. Ekkor a négyzetreemelés ekvivalens átalakítás, az eredeti egyenlőtlenség is fennáll.   2. eset. Ha $X^2-10X+21<0$, akkor a $3<X<7$ egyenlőtlenségeknek kell teljesülni. Ebben az esetben az $X^2+\left(m-10\right)X+25=0$ egyenletet kell megoldanunk, aminek gyökei $\begin{array}{c}{\displaystyle X_3=\frac{-m+10+\sqrt[]{m^2-20m}}{2}\text{és}{X}_4=\frac{-m+10-\sqrt[]{m^2-20m}}{2}\mathrm{.}}\end{array}$ Csak akkor vannak valós gyökök, ha $m^2-20m\ge 0$, azaz ha $m\le 0$ vagy $20\le m$ teljesül. Ha $3<X_3<7$, akkor ezt átrendezve kapjuk, hogy $\begin{array}{c}{\displaystyle m-4<\sqrt[]{m^2-20m}<m+4\mathrm{.}}\end{array}$ Ha $m\le 0$, akkor a bal oldali egyenlőtlenség nyilván teljesül, a jobb oldaliból pedig négyzetreemelés és újabb rendezés után $m>-4/7$ következik. Ha ez teljesül, akkor $m+4>0$, ezért a négyzetreemelés ekvivalens átalakítás, az eredeti egyenlőtlenség is fennáll. Ha $m\ge 20$, akkor négyzetreemelés és rendezés után a bal oldali egyenlőtlenségből $m<-4/3$ adódik, tehát ez az egyenlőtlenség nem állhat fenn. Ha $3<X_4<7$, akkor ezt átrendezve kapjuk, hogy $\begin{array}{c}{\displaystyle \sqrt[]{m^2-20m}<-m+4\text{és}-m-4<\sqrt[]{m^2-20m}\mathrm{.}}\end{array}$ Ha $m\le 0$, akkor az első egyenlőtlenségből négyzetreemelés és újabb rendezés után $m>-4/3$ következik. Ha ez teljesül, akkor $m+4>0$, ezért a négyzetreemelés ekvivalens átalakítás, az eredeti egyenlőtlenség is fennáll, a második egyenlőtlenség pedig nyilván teljesül, ha $-4/3<m\le 0$. Ha $m\ge 20$, akkor az első egyenlőtlenség jobb oldalán negatív szám áll, tehát ekkor nem teljesülhet az egyenlőtlenség. A kapott eredményeinket a következő táblázatban foglalhatjuk össze:   ${\displaystyle \begin{array}{|cc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi></math> értéke }}\hfill & \hfill {\displaystyle \text{ megoldások száma }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mn>10</mn><mo stretchy="false">-</mo><mrow><mroot><mrow><mn>68</mn></mrow><mrow></mrow></mroot></mrow></math> }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mn>10</mn><mo stretchy="false">-</mo><mrow><mroot><mrow><mn>68</mn></mrow><mrow></mrow></mroot></mrow></math> }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>10</mn><mo stretchy="false">-</mo><mrow><mroot><mrow><mn>68</mn></mrow><mrow></mrow></mroot></mrow><mo stretchy="false"><</mo><mi>m</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math> }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math> }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow><mo stretchy="false"><</mo><mi>m</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>7</mn></mrow></mfrac></mrow></math> }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>7</mn></mrow></mfrac></mrow></math> }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>7</mn></mrow></mfrac></mrow><mo stretchy="false"><</mo><mi>m</mi><mo stretchy="false"><</mo><mn>0</mn></math> }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mo stretchy="false">=</mo><mn>0</mn></math> }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mo stretchy="false"><</mo><mi>m</mi></math> }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill \\ \hline\end{array}}$