Feladat:	B.4657	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Telek Máté László
Füzet:	2015/május, 280 - 282. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Háromszög nevezetes körei
Hivatkozás(ok):	Feladatok: 2014/október: B.4657

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Induljunk ki a feltételből és alakítsuk át, majd ismét használjuk fel az eredeti feltételt. 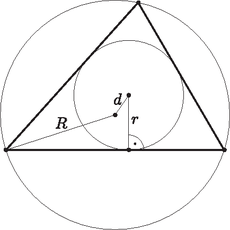Így kapjuk, hogy: ${\displaystyle \begin{array}{c}\hfill {\displaystyle R<r\left(\sqrt[]{2}+1\right)\mathrm{,}{R}^2<Rr\left(\sqrt[]{2}+1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle R^2-2Rr<Rr\left(\sqrt[]{2}-1\right)<r\left(\sqrt[]{2}+1\right)\cdot r\left(\sqrt[]{2}-1\right)=r^2\mathrm{.}}\hfill \end{array}}$     Euler tétele szerint, ha $d$ jelöli a háromszög beírható köre és körülírt köre középpontjának a távolságát, akkor $\begin{array}{c}{\displaystyle d^2=R^2-2Rr\mathrm{.}}\end{array}$ Feltételünkből tehát $d^2<r^2$, azaz $d<r$ következik. A két kör középpontjának a távolsága kisebb, mint a beírt kör sugara, ezért a körülírt kör középpontja a beírt kör belsejében, s így a háromszög belsejében van. Viszont egy háromszög körülírt körének középpontja pontosan akkor van a háromszög belsejében, ha a háromszög hegyesszögű. Tehát a $R<r\left(\sqrt[]{2}+1\right)$ feltételből következik, hogy a háromszög hegyesszögű.   II. megoldás. Megmutatjuk, hogy ha egy háromszögben teljesül az eredeti feltétel átalakításával kapott, azzal ekvivalens $\begin{array}{c}{\displaystyle \frac{r}{R}+1>\frac{1}{\sqrt[]{2}+1}+1=\sqrt[]{2}}\end{array}$ egyenlőtlenség, akkor a háromszög hegyesszögű. Jelölje a háromszög szögeit $\alpha$, $\beta$ és $\gamma$. Tudjuk, hogy $\begin{array}{c}{\displaystyle \frac{r}{R}+1=\text{cos}\alpha +\text{cos}\beta +\text{cos}\gamma }\end{array}$ (ennek bizonyítását lásd a megoldás utáni megjegyzésben). Ezért elég azt megmutatnunk, hogy ha a háromszög nem hegyesszögű, akkor $\begin{array}{c}{\displaystyle \text{cos}\alpha +\text{cos}\beta +\text{cos}\gamma \le \sqrt[]{2}\mathrm{.}}\end{array}$ Feltehetjük, hogy $\gamma$ a legnagyobb szög. Ekkor $\gamma \ge {90}^{\circ }$, és ezért $\alpha +\beta \le {90}^{\circ }$, továbbá $\text{cos}\gamma =-\text{cos}\left(\alpha +\beta \right)$. Tehát azt kell belátnunk, hogy $\begin{array}{c}{\displaystyle \text{cos}\alpha +\text{cos}\beta -\text{cos}\left(\alpha +\beta \right)\le \sqrt[]{2}\mathrm{.}}\end{array}$ A koszinuszok összegére vonatkozó képletet alkalmazva, felhasználva, hogy $0<\text{cos}\frac{\alpha -\beta }{2}\le 1$, végül pedig a kétszeres szög koszinuszának képletét használva kapjuk, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{cos}\alpha +\text{cos}\beta -\text{cos}\left(\alpha +\beta \right)}& {\displaystyle =2\text{cos}\frac{\alpha +\beta }{2}\text{cos}\frac{\alpha -\beta }{2}-\text{cos}\left(\alpha +\beta \right)}\hfill \\ \hfill {\displaystyle }& {\displaystyle \le 2\text{cos}\frac{\alpha +\beta }{2}-2\text{cos}{}^2\frac{\alpha +\beta }{2}+1.}\hfill \end{array}}$ Bevezetve a $\delta =\frac{\alpha +\beta }{2}$ jelölést azt kell tehát megmutatnunk, hogy ha $0^{\circ }\le \delta \le {45}^{\circ }$, azaz $1\ge \text{cos}\delta \ge \sqrt[]{2}/2$, akkor $\begin{array}{c}{\displaystyle 2\text{cos}\delta -2\text{cos}{}^2\delta +1\le \sqrt[]{2}\mathrm{.}}\end{array}$ Ez rendezés és teljes négyzetté kiegészítés után ekvivalens a $\begin{array}{c}{\displaystyle 0\le {\left(\text{cos}\delta -\frac{1}{2}\right)}^2+\frac{2\sqrt[]{2}-3}{4}}\end{array}$ egyenlőtlenséggel. A $\text{cos}\delta$-ra vonatkozó feltétel miatt itt a jobb oldal akkor a legkisebb, ha $\text{cos}\delta =\sqrt[]{2}/2$, s értéke ekkor $0$. Vagyis az egyenlőtlenség mindig fennáll, ami bizonyítja állításunkat.   Megjegyzés. Ha a háromszög oldalait a szokásos módon $a$, $b$ és $c$, kerületét $2s$, területét pedig $T$ jelöli, akkor az ismert $r=\frac{T}{s}$ és $R=\frac{abc}{4T}$ összefüggéseket és Héron képletét felhasználva kapjuk, hogy $\begin{array}{c}{\displaystyle \frac{r}{R}+1=\frac{4T^2}{sabc}+1=\frac{\left(-a+b+c\right)\left(a-b+c\right)\left(a+b-c\right)+2abc}{2abc}\mathrm{.}}\end{array}$ (1) A szögek koszinuszait a koszinusztételből kifejezve majd közös nevezőre hozva pedig azt kapjuk, hogy ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle \text{cos}\alpha +\text{cos}\beta +\text{cos}\gamma }& {\displaystyle =\frac{b^2+c^2-a^2}{2bc}+\frac{a^2+c^2-b^2}{2ac}+\frac{a^2+b^2-c^2}{2ab}=}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle }& {\displaystyle =\frac{-a^3-b^3-c^3+a{b}^2+a{c}^2+b{a}^2+b{c}^2+c{a}^2+c{b}^2}{2abc}\mathrm{.}}\hfill \end{array}}$ Ezután egyszerű számolással ellenőrizhető, hogy az (1) és (2) egyenlőségek jobb oldalán álló kifejezések megegyeznek, ami bizonyítja a feladat megoldásában felhasznált azonosságot.