Feladat:	B.4642	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Varga-Umbrich Eszter
Füzet:	2015/május, 277 - 278. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Kombinatorikus geometria, Síkgeometriai bizonyítások, Háromszögek geometriája
Hivatkozás(ok):	Feladatok: 2014/szeptember: B.4642

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Válasszunk ki a pontok közül négyet. Ezt $\left(\genfrac{}{}{0ex}{}{5}{4}\right)=5$-féleképpen tehetjük meg. A kiválasztott pontok (amiket jelöljön $A$, $B$, $C$ és $D$) vagy egy konvex-, vagy egy konkáv négyszög csúcsait adják meg. Bármely négyszögben a belső szögek összege ${360}^{\circ }$. Ha a négyszög konvex, akkor legnagyobb szöge legalább $\frac{{360}^{\circ }}{4}={90}^{\circ }$. Ha ez pl. a $B$ csúcsnál van (1. ábra), akkor az öt pont által meghatározott háromszögek közül az $ABC$ biztosan nem hegyesszögű. Ha a négyszög konkáv, akkor feltehetjük, hogy a $B$-nél lévő belső szöge nagyobb mint ${180}^{\circ }$ (2. ábra). Ezt a szöget a $BD$ átló két részre osztja, ha ezek közül pl. az $ABD\sphericalangle$ a nagyobb, akkor az $ABD$ háromszög tompaszögű. 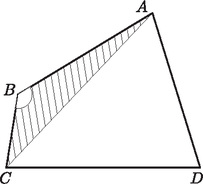  1. ábra 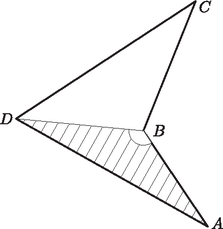    2. ábra   Tehát bármely négy pontot is választjuk, az általuk meghatározott $\left(\genfrac{}{}{0ex}{}{4}{3}\right)=4$ háromszög közül legalább az egyik nem hegyesszögű. Az öt kiválasztás közül bármelyik ponthármas pontosan kettőben szerepel együtt (az $A$, $B$, $C$ hármashoz vagy $D$-t, vagy az ötödik, $E$ pontot választhatjuk negyediknek), tehát egy adott nem hegyesszögű háromszöget legfeljebb két választásnál számolunk. Vagyis az öt pont által meghatározott nem hegyesszögű háromszögek száma legalább $5/2=2\mathrm{,}5$. De mivel ez a szám nyilván egész, ebből az is következik, hogy legalább $3$. Tehát az öt pont által meghatározott $10$ háromszög között legfeljebb $10-3=7$ hegyesszögű van.