Feladat:	B.4647	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Tomcsányi Gergely
Füzet:	2015/április, 214 - 215. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Körök, Lefedések, Esetvizsgálat
Hivatkozás(ok):	Feladatok: 2014/szeptember: B.4647

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Legyen a lefedett kör $k$, középpontja $O$, a legalsó pontja $A$. Az $A$ pontot lefedi egy kör, ez legyen a $k_1$, ennek a középpontja legyen $O_1$ és a legfelső pontja $F$. $OA\parallel {FO}_1$ és $OA={FO}_1=1$, ezért az $AO{FO}_1$ négyszög paralelogramma. Jelöljük az ${AO}_1$ szakasz hosszát $x$-szel. A $k_1$ kör lefedi az $A$ pontot, ezért $x\le 1$. Így $OF=x\le 1$, tehát a $k$ kör lefedi $F$-et. Jelölje az $F$-hez legközelebbi kör középpontját $O_2$, és legyen ${FO}_2=d$. Ha $d\le 1$, akkor $F$ le van fedve. A továbbiakban legyen $d>1$. Ha $x<1$, akkor rajzoljunk egy $F$ középpontú, $\varrho =\underset{}{\overset{}{\text{min}}}\left(1-x\mathrm{,}d-1\right)$ sugarú kört, legyen ez $k_3$ (1. ábra). Mivel $d>1$, így $k_3$ egyetlen belső pontját sem fedi le $k_1$-től különböző kör a 100 kör közül, és a $k_1$ nem fedi le az egészet, így $k_3$ nincs teljesen lefedve. Mivel $k_3\subset k$, így $k$ sincs teljesen lefedve. Ez ellentmondás, tehát ez az eset nem jöhet létre. 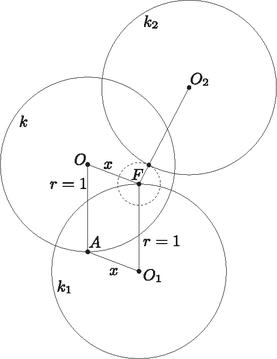  1. ábra   Ha $x=1$, akkor $k$ áthalad az $F$ ponton. Rajzoljunk egy $F$ középpontú, $\varrho =d-1$ sugarú kört, legyen ez $k_3$ (2. ábra). Mivel $k$ és $k_1$ egybevágó, de különböző körök, így $k_3$-on belüli részeik is egybevágóak, de különbözőek. Így $k$-nak lesz olyan $k_3$-on belüli pontja, amit nem fed le a $k_1$ és a többi kör sem, mert $k_2$ a legközelebbi kör. Ez is ellentmondás, tehát ez az eset sem lehetséges. 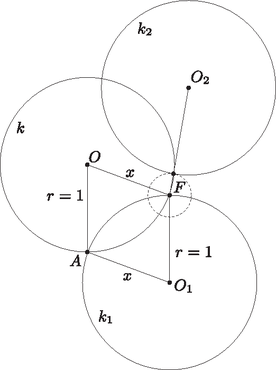  2. ábra   Vagyis $d$ sosem nagyobb 1-nél. Tehát a lefedett kör legalsó pontját lefedő kör legfelső pontja mindig le van fedve.