Feladat:	B.4661	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Adorján Dániel ,  Baran Zsuzsanna
Füzet:	2015/április, 218 - 219. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Logikai feladatok
Hivatkozás(ok):	Feladatok: 2014/november: B.4661

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Ha minden korongnak legfeljebb három szomszédja van, vagyis legfeljebb három másik korongot ,,lát'' a táblán, akkor ez azt jelenti, hogy legalább egy irányban nincs szomszédja. Mondhatjuk úgy, kinéz a tábláról egy ablakon, ahol az ,,ablak'' a sakktábla kerületének egységnyi része. Megállapíthatjuk, hogy a sarokba bármilyen elrendezés mellett elhelyezhető korong anélkül, hogy bármely más korong kilátását zavarná. Ez azért igaz, mert a szélső sorokban és oszlopokban álló korongok közvetlenül kilátnak a tábláról, hiszen egyik oldaluk a tábla kerületén van. A sarkokba elhelyezett négy korong összesen 8 ablakot takar el. Ezután marad még $2\left(n+k\right)-8$ ablak. A legtöbb korongot akkor tudjuk elhelyezni, ha mindegyik pontosan egy ablakon lát ki. Ilyen elrendezés létezik, például ha az összes szélső mezőt korongokkal töltjük fel. Ebből további jó megoldásokat generálhatunk, a szélső korongok beljebb tologatásával, de újabb korongot már nem tudunk elhelyezni (ábra). 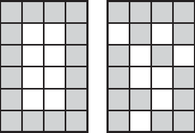    Megállapítható, hogy $n\mathrm{,}k\ge 2$ esetén a korongok száma legfeljebb $2\left(n+k\right)-4$ lehet. Ha $n=1$ vagy $k=1$, akkor legfeljebb annyi korong helyezhető el a táblán, ahány mező van, ilyenkor minden korongnak legfeljebb két szomszédja van.   II. megoldás. Az, hogy egy korongnak hány szomszédja van, azt mutatja meg, hogy az ,,oszlopában fölötte'', ,,oszlopában alatta'', ,,sorában tőle balra'', illetve a ,,sorában tőle jobbra'' irányok közül hányban van másik korong. Vegyünk egy olyan elrendezést, ahol a lehető legtöbb korong van a táblán úgy, hogy minden korongnak legfeljebb három szomszédja van. Ekkor minden sarokban kell lennie korongnak, mert ha valamelyikben nem lenne, oda téve még egy korongot egy több korongból álló megfelelő elrendezést kapnánk. (A sarokba tett korongnak legfeljebb két szomszédja lehet. Az elhelyezéssel csak olyan korongok szomszédjainak a száma nőhet, amelyek szélső sorban vagy oszlopban vannak, így a szomszédságaik száma nem nőhet 3 fölé.) Jelöljük meg azokat a korongokat, amelyek fölött abban az oszlopban már nincs másik korong. Ez oszloponként legfeljebb 1, így összesen legfeljebb $n$ db jelölést jelent. Most jelöljük meg azokat, amik a saját oszlopukban a legalsók, ez megint legfeljebb $n$ db jelölés. Jelöljük meg azokat is, amik a sorukban az elsők, ezekből legfeljebb $k$ db van, majd azokat is, amik a sorukban az utolsók, ezekből is legfeljebb $k$ db van. Ez összesen legfeljebb $2k+2n$ db jelölés, de a sarkokban lévő korongokat kétszer jelöltük meg. Ezek szerint legfeljebb $2k+2n-4$ db megjelölt korong lehet. Jelöletlen korong nem maradhatott, mert ha lenne, az azt jelentené, hogy az oszlopában alatta és fölötte és a sorában előtte és mögötte is van másik korong, azaz négy szomszédja van. Tehát legfeljebb $2k+2n-4$ korong helyezhető el a táblán megfelelő módon. Ha $n\mathrm{,}k\ge 2$, akkor ennyi valóban elhelyezhető, például ha az összes szélső mezőt korongokkal töltjük fel. Ekkor a sarkokban lévő korongoknak két, a többinek pedig három szomszédja lesz. Ha $k=1$ vagy $n=1$, akkor legfeljebb annyi korong helyezhető el a táblán, ahány mező van. Ilyenkor a két szélső korongnak egy-egy, a többinek két-két szomszédja lesz.