Feladat:	B.4569	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Badacsonyi István András ,  Balogh Tamás ,  Csépai András ,  Di Giovanni Márk ,  Fekete Panna ,  Frank György ,  Gyulai-Nagy Szuzina ,  Kabos Eszter ,  Kovács Márton ,  Maga Balázs ,  Mándoki Sára ,  Nagy-György Pál ,  Simkó Irén ,  Simon Kristóf ,  Viharos Loránd Ottó ,  Williams Kada
Füzet:	2015/április, 207 - 210. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Tetraéderek, Poliéderek egybevágósága, Esetvizsgálat, Szinusztétel alkalmazása, Trigonometriai azonosságok
Hivatkozás(ok):	Feladatok: 2013/október: B.4569

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.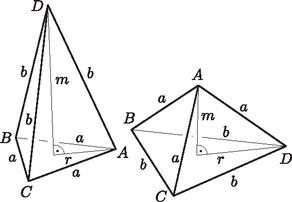   Megoldás. Vizsgáljuk meg, hogy az $a$ és $b$ hosszúságú élek egymáshoz képest hogyan helyezkedhetnek el egy $ABCD$ tetraéderben. Mivel a tetraédernek 4 csúcsa van, ezért biztosan van olyan csúcs, melyben legalább 2 darab $a$ hosszúságú él találkozik. Választhatjuk úgy a csúcsok jelölését, hogy $AB=AC=a$ legyen. Ha a harmadik $a$ hosszúságú él $BC$ vagy $AD$, akkor a tetraédernek van szabályos háromszöglapja, az első esetben $ABC$, a második esetben pedig $BCD$ (1. ábra). Ha a harmadik $a$ hosszúságú él nem $BC$ és nem is $AD$, akkor választhatjuk úgy a jelölést, hogy $BD$ hossza legyen $a$, ez a harmadik eset (2. ábra).   1. ábra 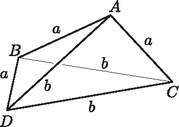    2. ábra   Meghatározzuk, hogy az egyes esetekben milyen $b/a$ arányok esetén létezik tetraéder. Az első és a második esetben legyen a szabályos háromszöglap körülírt körének sugara $r$, a kör középpontja $K$, ennek és a tetraéder negyedik csúcsának távolsága pedig $m$. Az $ADK$ háromszög a tetraéderek szimmetriája miatt mindkét esetben derékszögű, ezért Pitagorasz tétele szerint $m^2=A{D}^2-r^2$. Pontosan akkor létezik tetraéder, ha $m>0$, azaz $AD>r$ teljesül. Ismert, hogy ha egy szabályos háromszög oldalának hossza $h$, akkor a háromszög körülírt körének sugara $h\sqrt[]{3}/3$. Tehát az első esetben mindig létezik tetraéder, mert $b>a$ miatt $b>a\sqrt[]{3}/3$ mindig teljesül, a második esetben pedig pontosan akkor van ilyen tetraéder, ha $a>b\sqrt[]{3}/3$, azaz $a\sqrt[]{3}>b$ fennáll. A harmadik esetben először megkeressük azt az $a/b$ arányt, amikor a tetraéder négyszöggé fajul, azaz csúcsai egy síkba esnek. Ekkor az $ABDC$ négyszög oldalainak és átlóinak hosszát is ismerjük (3. ábra). Mivel megfelelő oldalaik hossza megegyezik, ezért a $CAB$ és $ABD$ háromszögek egybevágó egyenlőszárú háromszögek. Ebből következik, hogy $C$-nek az $AB$ szakasz felezőmerőlegesére vonatkozó tükörképe $D$, és ezért az $ABDC$ négyszög szimmetrikus trapéz. 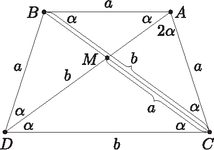  3. ábra   Ha tehát $ABC\sphericalangle =\alpha$, akkor $\begin{array}{c}{\displaystyle ACB\sphericalangle =BAD\sphericalangle =BDA\sphericalangle =\alpha \text{és}CAB\sphericalangle =ABD\sphericalangle ={180}^{\circ }-2\alpha \mathrm{.}}\end{array}$ A trapéz alapjainak párhuzamossága miatt $ABC\sphericalangle$ és $DCB\sphericalangle$ váltószögek, és így $DCA\sphericalangle =DCB\sphericalangle +BCA\sphericalangle =2\alpha$. Az $ADC$ és a $BCD$ háromszögek is egybevágó egyenlő szárú háromszögek, vagyis $DAC\sphericalangle =DCA\sphericalangle =2\alpha$. Az $ABC$ háromszögben a szögek összegét felírva kapjuk, hogy $\begin{array}{c}{\displaystyle {180}^{\circ }=ABC\sphericalangle +BCA\sphericalangle +\left(BAD\sphericalangle +DAC\sphericalangle \right)=\alpha +\alpha +\left(\alpha +2\alpha \right)=5\alpha \mathrm{,}}\end{array}$ amiből kapjuk, hogy $\alpha ={36}^{\circ }$. Ebből következik, hogy $DCA\sphericalangle ={72}^{\circ }$ és $ADC\sphericalangle ={36}^{\circ }$. Ha az $ABDC$ trapéz átlóinak metszéspontja $M$, akkor $MD=MC$, továbbá $\begin{array}{c}{\displaystyle AMC\sphericalangle ={180}^{\circ }-\left(BCA\sphericalangle +DAC\sphericalangle \right)={180}^{\circ }-\left({36}^{\circ }+{72}^{\circ }\right)={72}^{\circ }\mathrm{.}}\end{array}$ Tehát az $AMC$ háromszög is egyenlő szárú, $MC=AC=a$, és a szögek egyezősége miatt hasonló az $ADC$ háromszöghöz. Ezért a két háromszögben a megfelelő oldalak aránya megegyezik, vagyis $\begin{array}{c}{\displaystyle \frac{AD}{AC}=\frac{AC}{AM}=\frac{AC}{AD-MD}=\frac{AC}{AD-MC}\mathrm{,}\text{azaz}\frac{b}{a}=\frac{a}{b-a}\mathrm{.}}\end{array}$ Ebből rendezés után $\begin{array}{c}{\displaystyle {\left(\frac{b}{a}\right)}^2-\frac{b}{a}-1=0.}\end{array}$ A másodfokú egyenletet megoldva és figyelembe véve, hogy $b/a>1$, kapjuk hogy $\begin{array}{c}{\displaystyle \frac{b}{a}=\frac{1+\sqrt[]{5}}{2}\mathrm{.}}\end{array}$ Számolásunkból a szinusztételt és a megfelelő addíciós tételt alkalmazva következik, hogy $\begin{array}{c}{\displaystyle \frac{1+\sqrt[]{5}}{2}=\frac{AD}{AC}=\frac{\text{sin}{72}^{\circ }}{\text{sin}{36}^{\circ }}=2\text{cos}{36}^{\circ }\mathrm{,}}\end{array}$ ebből pedig kapjuk, hogy $\begin{array}{c}{\displaystyle \text{sin}{36}^{\circ }=\sqrt[]{1-\text{cos}{}^2{36}^{\circ }}=\sqrt[]{1-{\left(\frac{1+\sqrt[]{5}}{4}\right)}^2}=\frac{\sqrt[]{10-2\sqrt[]{5}}}{4}\mathrm{,}}\end{array}$ amiket a későbbiekben használni fogunk. Megmutatjuk, hogy pontosan akkor létezik a harmadik esetben leírt tetraéder, ha $\begin{array}{c}{\displaystyle 1<\frac{b}{a}<\frac{1+\sqrt[]{5}}{2}\mathrm{.}}\end{array}$ Ha létezik tetraéder, akkor a $D$ csúcs nincs benne az $ABC$ síkban. Forgassuk el a tetraéder $ABD$ lapját az $AB$ egyenes körül úgy, hogy a $D$ csúcs $D\text{'}$ képe az $ABC$ síkba kerüljön. Ekkor $ABD\text{'}C$ szimmetrikus trapéz, mert az $ABD\text{'}$ és $ABC$ háromszögek egybevágó egyenlőszárú háromszögek (4. ábra). Legyen $\gamma =ABC\sphericalangle =ACB\sphericalangle =BAD\text{'}\sphericalangle =BD\text{'}A\sphericalangle$. Mivel az $AB$ egyenes körül forgatunk, ezért a forgatás során a $D$ pont egy olyan $\text{S}$ síkban mozog, mely merőleges az $AB$ egyenesre. Ezért az $AB$-vel párhuzamos $CD\text{'}$ egyenes is merőleges $\text{S}$-re. Ez viszont azt jelenti, hogy $\text{S}$-nek a $C$-hez legközelebbi pontja $D\text{'}$, tehát $b=CD>CD\text{'}=c$. Mivel bármely háromszögben igaz, hogy nagyobb oldallal szemben nagyobb szög van, ezért ekkor 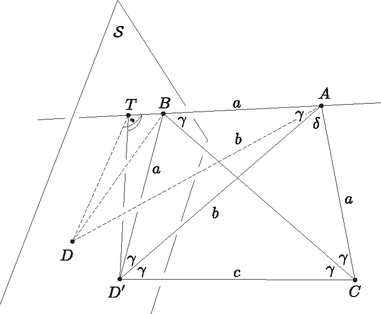$\begin{array}{c}{\displaystyle \delta =D\text{'}AC\sphericalangle <ACD\text{'}\sphericalangle =ACB\sphericalangle +BCD\text{'}\sphericalangle =ACB\sphericalangle +ABC\sphericalangle =2\gamma \mathrm{.}}\end{array}$ Vagyis az $ABC$ háromszögben a szögek összegére kapjuk, hogy ${180}^{\circ }=\delta +3\gamma <5\gamma$, tehát ${36}^{\circ }<\gamma$. Ezért a szinusztétel alapján $\begin{array}{c}{\displaystyle \frac{b}{a}=\frac{AD\text{'}}{AC}=\frac{\text{sin}2\gamma }{\text{sin}\gamma }=2\text{cos}\gamma <2\text{cos}{36}^{\circ }=\frac{1+\sqrt[]{5}}{2}\mathrm{.}}\end{array}$   4. ábra   Megfordítva, ha $1<\frac{b}{a}<\frac{1+\sqrt[]{5}}{2}$ teljesül, akkor legyen $D\text{'}$ az $ABC$ sík azon pontja, melyre $ABD\text{'}C$ szimmetrikus trapéz. A $b>a$ feltételből következik, hogy az $AB$ felezőmerőlegese által meghatározott két félsík közül $B$ és $D\text{'}$ az egyikben, $A$ és $C$ pedig a másikban van. Jelölje $\gamma$ és $\delta$ ugyanazokat a szögeket, mint az előző bekezdésben. Az $ABC$ egyenlőszárú háromszögből kapjuk, hogy $\begin{array}{c}{\displaystyle \text{cos}\gamma =\frac{\frac{BC}{2}}{AB}=\frac{b}{2a}\mathrm{.}}\end{array}$ Tehát $\begin{array}{c}{\displaystyle \frac{1}{2}<\text{cos}\gamma <\frac{1+\sqrt[]{5}}{4}\mathrm{,}\text{azaz}{60}^{\circ }>\gamma >{36}^{\circ }\mathrm{.}}\end{array}$ Ezért $\begin{array}{c}{\displaystyle D\text{'}AC\sphericalangle =\delta ={180}^{\circ }-3\gamma <{72}^{\circ }<2\gamma =D\text{'}CA\sphericalangle \mathrm{.}}\end{array}$ S mivel bármely háromszögben nagyobb szöggel szemben nagyobb oldal van, ezért $CD\text{'}<AD\text{'}=b$. Ha a $D\text{'}$-ből az $AB$ egyenesre állított merőleges talppontja $T\mathrm{,}$ akkor $\begin{array}{c}{\displaystyle D\text{'}T=b\text{sin}\gamma >b\text{sin}{36}^{\circ }=b\frac{\sqrt[]{10-2\sqrt[]{5}}}{4}\mathrm{.}}\end{array}$ Forgassuk az $ABD\text{'}$ háromszöget az $AB$ egyenes körül valamelyik irányban. A forgatás során $D\text{'}$ egy olyan $T$ középpontú körvonalon mozog, melynek síkja merőleges az $AB$ egyenesre és a $CD\text{'}$ távolság nyilván folytonosan változik. Amikor az elforgatás szöge éppen ${180}^{\circ }\mathrm{,}$ azaz a $D\text{'}$ pont átkerül $D\text{'}$-nek az $AB$ egyenesre vonatkozó $D\text{'}\text{'}$ tükörképébe, akkor a $CD\text{'}D\text{'}\text{'}$ derékszögű háromszögből kapjuk, hogy $\begin{array}{c}{\displaystyle CD\text{'}\text{'}>D\text{'}D\text{'}\text{'}=2D\text{'}T>b\frac{\sqrt[]{10-2\sqrt[]{5}}}{2}>b\mathrm{.}}\end{array}$ Ezért a forgatás során lesz egy olyan helyzet, amikor $D\text{'}$ képének és $C$-nek a távolsága $b$. Az ehhez a helyzethez tartozó $ABCD$ tetraéder eleget tesz a feltételeknek. A két tetraéder egybevágósága pontosan akkor következik a feladat feltételeiből, ha a három eset közül csak az egyikben leírt tetraéder valósítható meg. Mivel az első esethez tartozó tetraéder minden $b>a$ értékre létezik, ezért azt kell megnéznünk, hogy a másik két eset mikor nem építhető meg. A létezés feltétele a második esetben $b/a<\sqrt[]{3}$, a harmadikban pedig $b/a<\frac{1+\sqrt[]{5}}{2}$. Mivel $\sqrt[]{3}>\frac{1+\sqrt[]{5}}{2}$, ezért a két tetraéder egybevágóságának feltétele a $b/a\ge \sqrt[]{3}$ egyenlőtlenség teljesülése.