Kezdőlap


Feladat:	B.4566	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balogh Tamás , Barabás Ábel , Di Giovanni Márk , Egyházi Anna , Fekete Panna , Geng Máté , Kabos Eszter , Kocsis Júlia , Kúsz Ágnes , Lajkó Kálmán , Leipold Péter , Machó Bónis , Maga Balázs , Nagy-György Pál , Nagy-György Zoltán , Schwarcz Tamás , Varga Rudolf , Viharos Loránd Ottó , Williams Kada
Füzet:	2015/április, 204 - 206. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Vektorok, Pont körüli forgatás, Feladat, Konstruktív megoldási módszer
Hivatkozás(ok):	Feladatok: 2013/október: B.4566

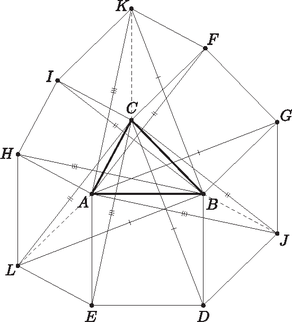
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $A B C$ , $K C F$ , $C K I$ , $H L A$ , $E A L$ , $B D J$ és $J G B$ háromszögek egybevágóak, hiszen két azonos hosszúságú oldaluk egyenlő szöget zár be. (Például $L E = H A = C A$ , $A E = A B$ , valamint

\begin{matrix} H A E ∢ & = 360^{\circ} - 90^{\circ} - 90^{\circ} - C A B ∢ = \\ = 180^{\circ} - C A B ∢, \end{matrix}

tehát

\begin{matrix} L E A ∢ = 180^{\circ} - H A E ∢ = C A B ∢ . \end{matrix}

A többi háromszögre is hasonlóan bizonyítható.) Az ábrán az egyvonalas, a kétvonalas, illetve a háromvonalas szakaszok páronként megkaphatóak egymásból egy valamelyik oldal hosszával, arra merőlegesen való eltolásból, illetve máshogy párosítva

90^{\circ}

-os elforgatással. Például

\begin{matrix} F C K ▵ ≅ C B A ▵, K C F ∢ = A B C ∢ és F C ⊥ C B, \end{matrix}

ezért az

F C K

háromszöget

90^{\circ}

-os forgatás viszi a

C B A

háromszögbe, vagyis

C K ⊥ B A

és egyenlő vele. Hasonlóan

L A ⊥ B C

és

L A = B C

, valamint

J B ⊥ A C

és

J B = A C

. Mindebből következik, hogy

C K ∥ B D

és

C K = B D

, vagyis

D B K C

paralelogramma, így

D C = B K

. Hasonlóan

L B = A G

L C = A F

B I = J C

J A = B H

E C = A K

. Másrészt

A B G ▵ ≅ K C B ▵

, mert három oldaluk egyenlő. Mivel

A B ⊥ K C

, így a két háromszög

90^{\circ}

-os forgatással megkapható egymásból, így

A G ⊥ K B

is teljesül. Hasonlóan látható be a többi szakaszra is a merőlegesség.

Ezekből következik, hogy

A K B ∢ = J A G ∢

(háromvonalas‐egyvonalas szög). Ugyanígy

B L C ∢ = G A F ∢

(egyvonalas‐kétvonalas szög), valamint

C J A ∢ = F A K ∢

(kétvonalas‐háromvonalas szög).
Tehát

A K B ∢ + B L C ∢ + C J A ∢ = J A G ∢ + G A F ∢ + F A K ∢ = J A K ∢

, ami két háromvonalas szakasz által bezárt szög, melyek egymásból

90^{\circ}

-os elforgatással kaphatók, tehát

J A K ∢ = 90^{\circ}

.
Ezzel az állítást beláttuk.

Megjegyzések: 1. A

B

-nél lévő egyvonalas, illetve a

C

-nél lévő kétvonalas

90^{\circ}

-os szögbe ugyanígy átforgathattuk volna a három szöget. 2. Hasonlóan belátható, hogy

E C D ∢ = J A G ∢

és

I B H ∢ = F A K ∢

, amiből látszik, hogy a feladat ekvivalens egy könnyebben megfogalmazható állítással: Ha egy tetszőleges

A B C

háromszögre kifele

A B D E

B C F G

és

C A H I

négyzeteket rajzolok, akkor

F A G ∢ + H B I ∢ + E C D ∢ = 90^{\circ}

.

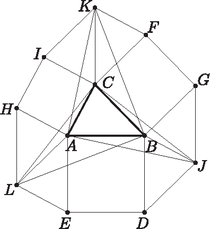
II. megoldás.

B D J ▵ ≅ A B C ▵

, mert

D

-nél és

B

-nél ugyanakkora szögek vannak és

A B = B D

, illetve

B C = D J

. Hasonlóan

B D J ▵ ≅ C K I ▵ ≅ H L A ▵ ≅ A B C ▵

. Ezért

A L = a

B J = b

és

C K = c

B J C ▵ ≅ A C L ▵

, mert

B J = A C

B C = A L

és

J B C ∢ = γ + 90^{\circ} = L A C ∢

. Hasonlóan

A B L ▵ ≅ C K B ▵

és

A B J ▵ ≅ K C A ▵

.
A bizonyítás további részében irányított szögekkel számolunk. Az eddigiekből következik, hogy

\begin{matrix} B L C ∢ + A K B ∢ + C J A ∢ = \\ = & B L A ∢ + A L C ∢ + A K C ∢ + C K B ∢ + C J B ∢ + B J A ∢ = \\ = & K B C ∢ + B C J ∢ + J A B ∢ + A B L ∢ + L C A ∢ + C A K ∢ . \end{matrix}

Tekintsük az

A K B

, a

B L C

és a

C J A

háromszögek belső szögeinek összegét:

\begin{matrix} 3 \cdot 180^{\circ} & = & B A K ∢ + A K B ∢ + K B A ∢ + B L C ∢ + L C B ∢ + C B L ∢ + \\ + C J A ∢ + J A C ∢ + A C J ∢ = \\ = & (A K B ∢ + B L C ∢ + C J A ∢) + (α + C A K ∢) + (β + K B C ∢) + \\ + (γ + L C A ∢) + (β + A B L ∢) + (α + J A B ∢) + (γ + B C J ∢) = \\ = & (A K B ∢ + B L C ∢ + C J A ∢) + (2 α + 2 β + 2 γ) + \\ + (C A K ∢ + K B C ∢ + L C A ∢ + A B L ∢ + J A B ∢ + B C J ∢) = \\ = & (A K B ∢ + B L C ∢ + C J A ∢) + 2 \cdot 180^{\circ} + (A K B ∢ + B L C ∢ + C J A ∢) . \end{matrix}

Tehát

180^{\circ} = 2 (A K B ∢ + B L C ∢ + C J A ∢)

, azaz

90^{\circ} = A K B ∢ + B L C ∢ + C J A ∢

, és ezt kellett bizonyítani.

Megjegyzés. Nagyon sok megoldó az ábra miatt olyan következtetésre jutott, ami általános háromszögre nem teljesül. Ezt esetszétválasztással vagy irányított szögek használatával lehetett kiküszöbölni.

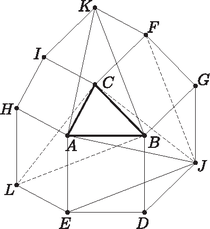
III. megoldás. Egy

\vec{v}

vektor

90^{\circ}

-kal való elforgatottját jelölje

\vec{v}'

, egy

P

pontét pedig

P'

Ekkor

\begin{matrix} \vec{A K} & = \vec{A C} + \vec{C I} + \vec{I K} = - \vec{C A} + \vec{C A}' + \vec{C F} = \\ = - \vec{C A} + \vec{C A}' + \vec{B C}', \end{matrix}

amiből

\begin{matrix} \vec{A K}' & = (- \vec{C A} + \vec{C A}' + \vec{B C}')' = \\ = (- \vec{C A})' + (\vec{C A}')' + (\vec{B C}')' = \\ = - \vec{C A}' - \vec{C A} - \vec{B C} . \end{matrix}

Felírható, hogy

\vec{A J} = \vec{A B} + \vec{B D} + \vec{D J} = \vec{A B} + \vec{A B}' + \vec{B C}'

.
Tudjuk, hogy

\vec{A B} + \vec{B C} + \vec{C A} = \vec{0}

, és így

\begin{matrix} (\vec{A B} + \vec{B C} + \vec{C A})' = \vec{A B}' + \vec{B C}' + \vec{C A}' = \vec{0}' = \vec{0}, \end{matrix}

így

\vec{A B}' + \vec{B C}' = - \vec{C A}'

és

\vec{A B} = - \vec{B C} - \vec{C A}

, tehát

\vec{A K}' = \vec{A J}

. Tehát a

K

pont

A

körüli

- 90^{\circ}

-os elforgatottja a

J

pont, a

B

pont elforgatottja az

E

pont, ezért az

A K B ▵

elforgatottja az

A J E ▵

. Emiatt

A K B ∢ = A J E ∢

.
Hasonlóan belátható, hogy a

B L C ▵

C

körüli

+ 90^{\circ}

-os elforgatottja az

F J C ▵

, ami miatt

B L C ∢ = F J C ∢

.
Tehát

A K B ∢ + B L C ∢ + C J A ∢ = A J E ∢ + F J C ∢ + C J A ∢ = F J E ∢

. Erről kéne belátni, hogy

90^{\circ}

. Mivel

\vec{J E} = \vec{J D} + \vec{D E}

, így

\begin{matrix} \vec{J E}' = (\vec{J D} + \vec{D E})' = (\vec{G B} + \vec{D E})' = \vec{G B}' + \vec{D E}' = \vec{G F} + \vec{D B} = \vec{G F} + \vec{J G} = \vec{J F} . \end{matrix}

Tehát az

F

pont az

E

pont

J

körüli

- 90^{\circ}

-os elforgatottja. Ezzel beláttuk, hogy

F J E ∢ = 90^{\circ}

, a bizonyítást befejeztük.