Feladat:	4863. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Mocskonyi Mirkó
Füzet:	2016/december, 569 - 570. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Egyéb áram mágneses tere
Hivatkozás(ok):	Feladatok: 2016/szeptember: 4863. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.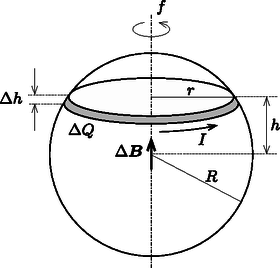   Megoldás. Jelöljük a gömb átmérőjét $d$-vel ($d=2R$), felületi töltéssűrűségét $\sigma$-val, fordulatszámát $f$-fel, és tételezzük fel, hogy a gömb anyagának relatív permeabilitása ${\mu }_{\text{r}}\approx 1$.     Osszuk fel a gömb felületét a forgástengelyre merőleges síkmetszetekkel sok kicsi (igen keskeny) gömbövre. Egy-egy gömböv pontjai (jó közelítéssel) azonos kerületi sebességgel mozognak, tehát mindegyik töltött, forgó gömböv körvezetőnek (egymenetű tekercsnek) tekinthető. Ezek a körvezetők a gömb középpontjában a forgástengellyel párhuzamos (a jobbkéz-szabálynak megfelelő irányú) mágneses teret hoznak létre, az egész gömb mágneses tere pedig a körvezetők $\Delta \text{<span style="font-weight: bold;"><span style="font-style: italic;">B</span></span>}$ járulékának összege. Tekintsük azt a (nagyon vékony) gömbövet, amelyet határoló egyik kör (az ábrán látható módon) a forgástengelyre merőleges síkban, a gömb középpontjától $h$ távolságban helyezkedik el. Ennek a körnek a sugara $r=\sqrt[]{R^2-h^2}$. Ha a gömböv magassága $\Delta h\ll h$, akkor a gömböv felszíne $d\pi \Delta h$, a töltése pedig $\Delta Q=d\pi \sigma \Delta h$. Az $f$ fordulatszámmal forgó (tehát $\Delta t=1/f$ idő alatt körbeforduló) gömböv töltésének mozgása $I=f\Delta Q$ áramot képvisel, és ez a gömb középpontjában (a Biot‐Savart-törvény szerint) $\begin{array}{c}{\displaystyle \Delta B={\mu }_0\frac{I}{2}\frac{r^2}{R^3}={\mu }_0\frac{\sigma \pi f}{R^2}\left(R^2-h^2\right)\Delta h}\end{array}$ nagyságú mágneses teret hoz létre. A mágneses indukció nagysága a gömb középpontjában ezek szerint: $\begin{array}{c}{\displaystyle B=2\cdot {\mu }_0\frac{\sigma \pi f}{R^2}\sum _{h=0}^R\left(R^2-h^2\right)\Delta h\mathrm{.}}\end{array}$ (A kettes szorzó azt fejezi ki, hogy a teljes mágneses térhez a gömb alsó és felső felének gömbövei is adnak járulékot.) Az összeg (ami egy térfogat dimenziójú mennyiség) integrálszámítás segítségével, de ‐ Arkhimédész módszerét követve ‐ elemi megfontolásokkal is kiszámítható. $\begin{array}{c}{\displaystyle \sum _{h=0}^R\left(R^2-h^2\right)\Delta h=\sum _{h=0}^R{R}^2\Delta h-\sum _{h=0}^R{h}^2\Delta h\mathrm{.}}\end{array}$ A jobb oldal első tagja egy $R$ oldalú kocka térfogata, tehát $R^3$. A második tagban (ha a felosztást egyre finomabbra választjuk) felismerhetjük egy $R$ oldalú kockába írható, négyzet alapú gúla térfogatát, ami $\frac{1}{3}{R}^3$. A két összeg különbsége tehát $\frac{2}{3}{R}^3$. Az indukcióvektor nagysága a gömb középpontjában ezek szerint (a megadott számértékek felhasználásával): $\begin{array}{c}{\displaystyle B=\frac{2\pi }{3}{\mu }_0\sigma fd=2\mathrm{,}6\cdot {10}^{-11}\text{T. }}\end{array}$   Megjegyzés. A kiszámítandó összeg értéke természetesen integrálszámítással is megkapható: $\begin{array}{c}{\displaystyle \sum _{h=0}^R\left(R^2-h^2\right)\Delta h\approx \underset{0}{\overset{R}{\int }}\left(R^2-h^2\right)\text{d}h=\frac{2}{3}{R}^3\mathrm{.}}\end{array}$ A megoldók többsége ezt az utat követte, de ‐ mint a fenti megoldásból látható ‐ ,,elemi'' megfontolásokkal is eljuthatunk a végeredményhez. Arkhimédész módszerét, amivel már az ókorban ki tudta számítani egy gömb térfogatát, az integrálszámítás fontos előzményének tekintik. Azt, hogy a gömb térfogata a köré írt henger térfogatának $\frac{2}{3}$ része, Arkhimédész a legnagyobb felfedezésének tartotta. Ezért kérte, hogy halála után sírját egy hengerbe írt gömbbel jelöljék meg. Így is történt. Mintegy 200 évvel később Arkhimédész elhagyatott sírját ezen jel alapján találta meg Cicero. (‐ A szerk.)