Feladat:	2016. évi Nemzetközi Fizika Diákolimpia 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2016/november, 489 - 493. oldal		PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia, Merev testek dinamikája, Mozgásegyenletek gyorsuló koordináta-rendszerekben, Pontrendszer impulzusnyomatéka (perdülete)
Hivatkozás(ok):	Feladatok: 2016/október: 2016. évi Nemzetközi Fizika Diákolimpia 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. feladat. Két mechanikai probléma A rész. Elrejtett korong A.1. Egyensúlyban a testre ható erők és forgatónyomatékok eredője nulla. Az utóbbi feltétel a lejtővel való $P$ érintkezési pontra nézve úgy teljesíthető, ha a rendszer $C$ tömegközéppontja éppen a $P$ pont felett helyezkedik el (1. ábra). Alkalmazzuk a $PCS$ háromszögre a szinusztételt: 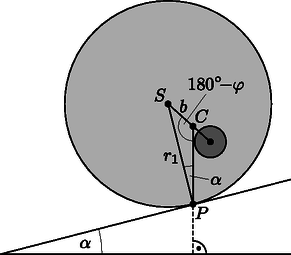$\begin{array}{c}{\displaystyle \frac{\text{sin}\left({180}^{\circ }-\phi \right)}{\text{sin}\alpha }=\frac{r_1}{b}\mathrm{,}}\end{array}$ ebből $\begin{array}{c}{\displaystyle b=\frac{r_1\text{sin}\alpha }{\text{sin}\phi }\mathrm{.}}\end{array}$   1. ábra   A.2. A korong $\phi$ szögkitérésekor a nehézségi erő forgatónyomatéka $Mgb\text{sin}\phi$, iránya pedig olyan, hogy a kitérést csökkenteni igyekszik. A forgómozgás egyenlete tehát a következő alakot ölti: $\begin{array}{c}{\displaystyle {\Theta }_S\ddot{\phi }=-Mgb\text{sin}\phi \mathrm{.}}\end{array}$ Kis szögekre $\text{sin}\phi \approx \phi$, így egy harmonikus rezgőmozgás (fizikai inga) mozgásegyenletét kapjuk: $\begin{array}{c}{\displaystyle \ddot{\phi }=-{\omega }^2\phi \mathrm{,}\text{ahol}\omega =\sqrt[]{\frac{Mgb}{{\Theta }_S}}\mathrm{.}}\end{array}$ A rezgés periódusideje a körfrekvenciával $T=2\pi /\omega$ kapcsolatban áll, így a tehetetlenségi nyomaték kifejezhető: $\begin{array}{c}{\displaystyle {\Theta }_S=\frac{T^2}{4{\pi }^2}Mgb\mathrm{.}}\end{array}$ A.3. Gondolkozhatunk úgy, hogy egy ${\varrho }_1$ sűrűségű, $r_1$ sugarú tömör (tehát lyuk nélküli) korong és egy ${\varrho }_2-{\varrho }_1$ sűrűségű, $r_2$ sugarú korong közös tömegközéppontjának helyét kell meghatároznunk. A távolságokat a nagyobb korong $S$ középpontjától mérve a tömegközéppont helyét megadó egyenlet: $\begin{array}{c}{\displaystyle b=\frac{\left({\varrho }_2-{\varrho }_1\right)r_2^2\pi h_2}{M}d\mathrm{,}\text{amiből}d=\frac{Mb}{\left({\varrho }_2-{\varrho }_1\right)r_2^2\pi h_2}\mathrm{.}}\end{array}$ A.4. Egy $m$ tömegű, $r$ sugarú korong tehetetlenségi nyomatéka $\frac{1}{2}m{R}^2$. Ennek és a Steiner-tételnek a felhasználásával írhatjuk, hogy $\begin{array}{c}{\displaystyle {\Theta }_S=\underset{\text{nagy korong}}{\overset{}{\underbrace{\frac{1}{2}{\varrho }_1{r}_1^4\pi h_1}}}+\underset{\text{kis korong a Steiner-tétellel}}{\overset{}{\underbrace{\left({\varrho }_2-{\varrho }_1\right)r_2^2\pi h_2\left(\frac{r_2^2}{2}+d^2\right)}}}\mathrm{.}}\end{array}$ A $d$-re az előző részfeladatban kapott eredményt felhasználva: $\begin{array}{c}{\displaystyle {\Theta }_S=\frac{1}{2}{\varrho }_1{r}_1^4\pi h_1+\frac{1}{2}\left({\varrho }_2-{\varrho }_1\right)r_2^4\pi h_2+\frac{M^2{b}^2}{\left({\varrho }_2-{\varrho }_1\right)r_2^2\pi h_2}\mathrm{.}}\end{array}$ A.5. Írjuk fel a teljes rendszer tömegét: $\begin{array}{c}{\displaystyle M={\varrho }_1{r}_1^2\pi h_1+\left({\varrho }_2-{\varrho }_1\right)r_2^2\pi h_2\mathrm{.}}\end{array}$ Ebből kifejezhetjük a $\left({\varrho }_2-{\varrho }_1\right)r_2^2\pi h_2$ tagot, és beírhatjuk az A.4. részfeladat végeredményébe. A ${\Theta }_S$-re korábban kapott formulát is felhasználva: $\begin{array}{c}{\displaystyle \frac{T^2}{4{\pi }^2}Mgb=\frac{1}{2}{\varrho }_1{r}_1^4\pi h_1+\frac{1}{2}\left(M-{\varrho }_1{r}_1^2\pi h_1\right)r_2^2+\frac{M^2{b}^2}{M-{\varrho }_1{r}_1^2\pi h_1}\mathrm{.}}\end{array}$ Ebből kifejezhető $r_2$: $\begin{array}{c}{\displaystyle r_2=\sqrt[]{\frac{2}{M-{\varrho }_1{r}_1^2\pi h_1}\left(\frac{T^2}{4{\pi }^2}Mgb-\frac{M^2{b}^2}{M-{\varrho }_1{r}_1^2\pi h_1}-\frac{1}{2}{\varrho }_1{r}_1^4\pi h_1\right)}\mathrm{.}}\end{array}$ Ennek ismeretében az össztömegből $h_2$ megkapható: $\begin{array}{c}{\displaystyle h_2=\frac{M-{\varrho }_1{r}_1^2\pi h_1}{\left({\varrho }_2-{\varrho }_1\right)r_2^2\pi }\mathrm{.}}\end{array}$   B rész. Forgó űrállomás B.1. A forgó űrhajó padlóján álló, $m$ tömegű testre az $mR{\omega }_0^2$ centrifugális erő hat. Ez akkor egyezik meg a test $m{g}_{\text{F}}$ földi súlyával, ha az űrállomás szögsebessége ${\omega }_0=\sqrt[]{g_{\text{F}}/R}$. B.2. Egy rugón rezgő test körfrekvenciája ${\omega }_{\text{F}}=\sqrt[]{k/m}$. B.3. Az űrhajón a mesterséges gravitáció egyenesen arányos a forgástengelytől mért távolsággal: $g\left(r\right)=r{\omega }_0^2$. A rugóra akasztott testet az egyensúlyi helyzetéből sugárirányban kifelé $x$ távolsággal kitérítve, arra nemcsak a rugóerő növekménye, hanem az effektív gravitációs tér megváltozásából származó erő is hat: $\begin{array}{c}{\displaystyle -kx+mx{\omega }_0^2=m\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}\mathrm{,}}\end{array}$ ami éppen olyan, mint egy $k^{*}=k-m{\omega }_0^2$ effektív direkciós erejű rugón rezgő test mozgásegyenlete, a rezgés körfrekvenciája tehát $\omega =\sqrt[]{k/m-{\omega }_0^2}$.   B.4. Az $M_{\text{F}}$ tömegű, $R_{\text{F}}$ sugarú Föld felszíne felett $h$ magasságban a gravitációs gyorsulás: $\begin{array}{c}{\displaystyle g_{\text{F}}\left(h\right)=\gamma \frac{M_{\text{F}}}{{\left(R_{\text{F}}+h\right)}^2}=\gamma \frac{M_{\text{F}}}{R_{\text{F}}^2}{\left(1+\frac{h}{R_{\text{F}}}\right)}^{-2}=g_{\text{F}}\left(0\right){\left(1+\frac{h}{R_{\text{F}}}\right)}^{-2}\mathrm{.}}\end{array}$ Mivel $h/R_{\text{F}}\ll 1$, alkalmazhatjuk a kis $\epsilon$ mennyiségekre érvényes ${\left(1+\epsilon \right)}^n\approx 1+n\epsilon$ lineáris közelítést: $\begin{array}{c}{\displaystyle g_{\text{F}}\left(h\right)\approx g_{\text{F}}\left(0\right)\left(1-\frac{2h}{R_{\text{F}}}\right)\mathrm{.}}\end{array}$ A földi gravitációs mezőben tehát az egyensúlyi helyzetéből $x$ távolságra kitérített test mozgásegyenlete $\begin{array}{c}{\displaystyle -kx+m{g}_{\text{F}}\frac{2x}{R_{\text{F}}}=m\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}\mathrm{,}}\end{array}$ amiből a rezgés körfrekvenciája $\begin{array}{c}{\displaystyle \widetilde{{\omega }_{\text{F}}}=\sqrt[]{\frac{k}{m}-\frac{2g_{\text{F}}}{R_{\text{F}}}}\mathrm{.}}\end{array}$ B.5. Az előző két részfeladat eredményéből látszik, hogy $\omega$ és $\widetilde{{\omega }_{\text{F}}}$ akkor egyezik meg, ha ${\omega }_0^2=2g_{\text{F}}/R_{\text{F}}$. A B.1. kérdés eredményét felhasználva ez azt jelenti, hogy az űrállomás sugarának hossza éppen a földsugár fele: $R=R_{\text{F}}/2$. B.6. A feladat megoldható inerciarendszerben is, ehelyett mi most a rövidebb, forgó koordináta-rendszerbeli leírást választjuk. A $H\ll R$ magasságból elengedett test ,,függőlegesen lefelé'' (azaz sugárirányban kifelé) mutató sebessége $t$ idejű esés után jó közelítéssel $v_y=R{\omega }_0^{2}t$. Az emiatt ,,vízszintes'' (érintő-)irányban ható Coriolis-erő nagysága tehát $F_{\text{C}}=2m{v}_y{\omega }_0=2mR{\omega }_0^{3}t$, a gyorsulás pedig $F_{\text{C}}/m$. A $v_x$ vízszintes sebességkomponenst az idő függvényében ennek a gyorsulásnak az integrálásával lehet meghatározni: $\begin{array}{c}{\displaystyle v_x\left(t\right)=\underset{0}{\overset{t}{\int }}2R{\omega }_0^{3}t\text{'}\text{d}t\text{'}=R{\omega }_0^3{t}^2\mathrm{.}}\end{array}$ Behelyettesítve az esés $T=\sqrt[]{2H/\left(R{\omega }_0^2\right)}$ idejét, megkapjuk a vízszintes sebességkomponenst a becsapódáskor: $\begin{array}{c}{\displaystyle v_x=2H{\omega }_0\mathrm{.}}\end{array}$ A vízszintes elmozdulást a $v_x\left(t\right)$ függvény integrálja adja meg: $\begin{array}{c}{\displaystyle d_x\left(t\right)=\underset{0}{\overset{t}{\int }}{v}_x\left(t\text{'}\right)\text{d}t\text{'}=\frac{1}{3}R{\omega }_0^3{t}^3\mathrm{.}}\end{array}$ A $t=T$ helyettesítéssel kapjuk meg a teljes vízszintes elmozdulást: $\begin{array}{c}{\displaystyle d_x=\frac{1}{3}\sqrt[]{\frac{8H^3}{R}}\mathrm{.}}\end{array}$ B.7. A mozgást inerciarendszerből a legegyszerűbb leírni. A $H=R\left(1-\text{cos}\phi \right)$ magasságú toronyból a test ${\omega }_{0}R\text{cos}\phi$ kezdősebességgel érintőirányban indul (2. ábra), és egyenes vonalú egyenletes mozgással halad egészen az űrállomás padlójáig. A mozgás ideje: 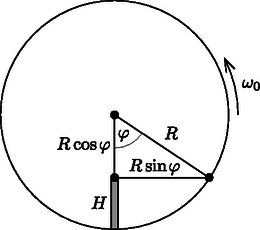$\begin{array}{c}{\displaystyle t=\frac{R\text{sin}\phi }{{\omega }_{0}R\text{cos}\phi }=\frac{\text{tg}\phi }{{\omega }_0}\mathrm{.}}\end{array}$ A test akkor érkezik éppen a torony aljához, ha ezalatt az idő alatt az űrállomás éppen $\phi$ szöggel fordul el, azaz $t=\phi /{\omega }_0$. Az időre kapott két egyenlet összevetéséből a $\phi =\text{tg}\phi$ egyenletet kapjuk. Ennek végtelen sok megoldása van: az első a triviális $\phi =0$, a többi pedig csak numerikusan határozható meg. A következő gyök $3\pi /2$ körüli érték, ami a nem releváns $H>R$ eredményre vezet. Az $5\pi /2$ környékén lévő harmadik gyök az, amit keresünk. Zsebszámológéppel a pontosabb $\phi \approx 7\mathrm{,}725$ radián értéket kaphatjuk. Ennek a szögnek a felhasználásával meghatározhatjuk a torony magasságát: $H\approx 0\mathrm{,}871R$.   2. ábra   B.8. Mivel az $y$ irányú Coriolis-erőt elhanyagolhatjuk, ebben az irányban a test harmonikus rezgőmozgást végez $d$ amplitúdóval. A kezdeti feltételeket is figyelembe véve: $y\left(t\right)=-d\text{cos}\omega t$. Az $y$ irányú sebességre ennek deriválásával $v_y\left(t\right)=d\omega \text{sin}\omega t$ értéket kapunk, amellyel az $x$ irányú Coriolis-erő (az űrállomás szögsebességvektorát a papír síkjába befelé mutatónak választva): 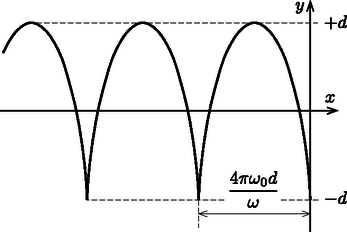$\begin{array}{c}{\displaystyle F_x\left(t\right)=-2m{v}_y\left(t\right){\omega }_0=-2m{\omega }_{0}d\omega \text{sin}\omega t\mathrm{.}}\end{array}$ A test gyorsulása $x$ irányban tehát éppen olyan, mint egy harmonikus oszcillátoré. Az $x$ irányú elmozdulást a gyorsulás kétszeri integrálásával kapjuk: $\begin{array}{c}{\displaystyle x\left(t\right)=\frac{2{\omega }_{0}d}{\omega }\text{sin}\omega t+c_{1}t+c_2\mathrm{,}}\end{array}$ ahol $c_1$ és $c_2$ integrálási állandók. A $t=0$ időpillanatban a test $x$ irányú sebessége és $x$ koordinátája is nulla, ebből $c_1=-2{\omega }_{0}d$ és $c_2=0$ adódik, tehát: $\begin{array}{c}{\displaystyle x\left(t\right)=\frac{2{\omega }_{0}d}{\omega }\left(\text{sin}\omega t-\omega t\right)\mathrm{.}}\end{array}$ A pálya vázlatos rajza a 3. ábrán látható.   3. ábra