Kezdőlap


Feladat:	B.4644	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Somogyi Pál , Telek Máté László
Füzet:	2015/március, 158 - 159. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai számítások trigonometria nélkül háromszögekben, Heron-képlet, Körérintők
Hivatkozás(ok):	Feladatok: 2014/szeptember: B.4644

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Húzzuk meg az $r$ és $R$ sugarú körök közös érintőit, és hosszabbítsuk meg az $R$ sugarú kör adott átmérőjét mindkét irányban (1. ábra). A keletkező $B C D$ háromszöget tükrözzük a $B D$ átfogójára. Az így létrejött $A B C D$ négyszög nyilvánvalóan négyzet, oldalai 2 $R$ hosszúa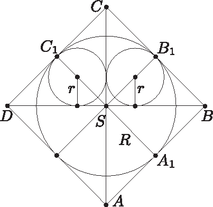k.

1. ábra

A négyzet területe:

T_{A B C D} = 4 R^{2}

.
Az

S B C

háromszög területe: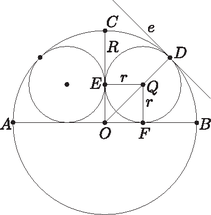

\begin{matrix} T_{S B C ▵} = \frac{T_{A B C D}}{4} = R^{2} . \end{matrix}

A Pitagorasz-tételt használva a négyzet átlója:

\begin{matrix} A C = \sqrt[]{{(2 R)}^{2} + {(2 R)}^{2}} = \sqrt[]{8 R^{2}} = 2 \sqrt[]{2} R, \end{matrix}

amiből

\begin{matrix} S B = S C = \frac{A C}{2} = \sqrt[]{2} R . \end{matrix}

T_{S B C ▵} = r \cdot s

, ahol

s

a félkerület:

\begin{matrix} s = \frac{S B + S C + B C}{2} = \frac{\sqrt[]{2} R + \sqrt[]{2} R + 2 R}{2} = \sqrt[]{2} R + R = R (\sqrt[]{2} + 1) . \end{matrix}

Ebből

\begin{matrix} r = \frac{T_{S B C ▵}}{s} = \frac{R^{2}}{R (\sqrt[]{2} + 1)} = \frac{R}{(\sqrt[]{2} + 1)} \cdot \frac{(\sqrt[]{2} - 1)}{(\sqrt[]{2} - 1)} = \frac{(\sqrt[]{2} - 1) R}{2 - 1} = (\sqrt[]{2} - 1) R . \end{matrix}

Tehát az

r

sugár hossza

(\sqrt[]{2} - 1) R

II. megoldás. Legyen

e

O

középpontú,

R

sugarú és a

Q

középpontú,

r

sugarú körök közös érintője (2. ábra). Az érintési pontban húzott sugár merőleges az érintőre, emiatt a

Q

pont rajta van az

O D

szakaszon:

\begin{matrix} O D = O Q + Q D = O Q + r = R . \end{matrix}

B O C ∢ = 90^{\circ}

, valamint az

O B

és

O C

szakaszok is érintői az

r

sugarú körnek, így

O F Q ∢ = O E Q ∢ = 90^{\circ}

, és

E Q = F Q = r

, ezért az

O F Q E

négyszög négyzet. A Pitagorasz-tételt használva a négyzet átlója:

\begin{matrix} O Q = \sqrt[]{r^{2} + r^{2}} = \sqrt[]{2} r . \end{matrix}

2. ábra

Tehát

\begin{matrix} R = O Q + r = \sqrt[]{2} r + r = r \cdot (\sqrt[]{2} + 1), \end{matrix}

amiből

\begin{matrix} r = \frac{R}{(\sqrt[]{2} + 1)} = \frac{R}{(\sqrt[]{2} + 1)} \cdot \frac{(\sqrt[]{2} - 1)}{(\sqrt[]{2} - 1)} = (\sqrt[]{2} - 1) R . \end{matrix}