Feladat:	B.4635	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csitári Nóra ,  Fonyó Viktória ,  Glattfelder Hanna ,  Kuchár Zsolt ,  Nagy-György Pál ,  Németh Hanna ,  Sal Kristóf ,  Szakács Lili Kata ,  Williams Kada
Füzet:	2015/március, 153. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai szerkesztések, Magasságpont, Körülírt kör, Húrnégyszögek
Hivatkozás(ok):	Feladatok: 2014/május: B.4635

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Legyen $P$ a kívánt tulajdonságú pont a $BC$ szakaszon. Ekkor $AOP\sphericalangle =PMA\sphericalangle$, amit jelöljünk $\beta$-val. Tükrözzük az $M$ pontot a $BC$ oldalra, tükörképe legyen $M\text{'}$, ami rajta van a háromszög köré írt körön. A tükrözés miatt $PMM\text{'}\sphericalangle =PM\text{'}M\sphericalangle$, melyet jelöljön $\alpha$. Mivel $AMP\sphericalangle +PMM\text{'}\sphericalangle =\beta +\alpha ={180}^{\circ }$, az $AOPM\text{'}$ négyszög húrnégyszög, hiszen két szemközti szögének összege: 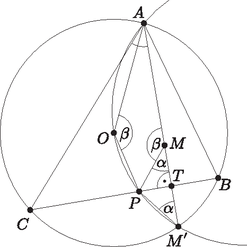$AOP\sphericalangle +PM\text{'}M\sphericalangle =\beta +\alpha ={180}^{\circ }$.     Ezek alapján a $P$ pont szerkesztése: Az $M$ magasságpontot tükrözzük a $BC$ oldalra, majd megszerkesztjük az $AOM\text{'}$ háromszög körülírt körét, ez a kör a $BC$ oldalt a $P$ pontban metszi. Mivel $AB<AC$, az $AOM\text{'}$ háromszög sosem lesz elfajuló, és mindig csak egy megoldás van, mivel a két körülírt kör $A$-ban és $M\text{'}$-ben metszi egymást, így az $ABC$ háromszög körülírt körén belül csak egy metszéspontja lehet az $AOM\text{'}$ háromszög köré írt körnek és a $BC$ oldalnak.