Feladat:	B.4617	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Scheidler Barnabás
Füzet:	2015/március, 145 - 147. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai szerkesztések, Súlyvonal, Thalesz tétel és megfordítása
Hivatkozás(ok):	Feladatok: 2014/március: B.4617

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.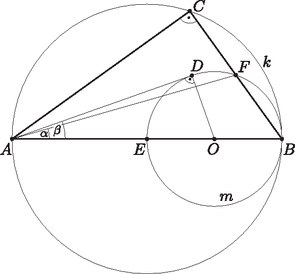   I. megoldás. Legyen az $ABC$ derékszögű háromszög $AB$ átfogójának felezőpontja $E$, $BC$ befogójának felezőpontja $F$, a befogóhoz tartozó súlyvonalnak és az $AB$ átfogónak a szöge $\alpha$, az $AB$ átfogó Thalész-köre $k$, ennek a $B$ középpontú, 1/2 arányú középpontos hasonlóságnál kapott képe pedig az $m$ kör. Ekkor $m$ az $EB$ szakasz Thalész-köre, középpontja az $AB$ szakasz $B$-hez legközelebbi $O$ negyedelőpontja (1. ábra).   1. ábra   Az $F$ pont felezi $BC$-t és $C$ rajta van $k$-n, ezért $F$ rajta van $m$-en, tehát az $AF$ egyenesnek és $m$-nek van közös pontja. Így $\alpha$ legfeljebb akkora, mint az $A$-ból $m$-hez húzott $AD$ érintő és $AB$ által bezárt $\beta$ szög. Ezt a szöget az $AOD$ derékszögű háromszögből határozhatjuk meg. $\begin{array}{c}{\displaystyle \text{sin}\beta =\frac{OD}{OA}=\frac{\frac{1}{4}AB}{\frac{3}{4}AB}=\frac{1}{3}\mathrm{,}\text{azaz}\beta =\text{arcsin}\frac{1}{3}\approx 19\mathrm{,}{47}^{\circ }\mathrm{.}}\end{array}$ Megmutatjuk, hogy minden $0^{\circ }<\alpha \le \text{arcsin}\frac{1}{3}$ esetén van olyan derékszögű háromszög, melyben az átfogó és az egyik befogóhoz tartozó súlyvonal szöge $\alpha$. Ha a feltétel teljesül, akkor az $AB$ egyenes egyik oldalára felmérve az $\alpha$ szöget, annak $AB$-tól különböző szára metszi $m$-et a $D_1$ és $D_2$ pontokban, illetve érinti $m$-et $D$-ben, ha $\alpha =\text{arcsin}\frac{1}{3}$ (2. ábra). Mivel $D_i$ rajta van $m$-en, azért ha $B$-ből kétszeresére nagyítjuk, akkor a kapott $D_i\text{'}$ pont rajta lesz $m$ kétszeresre nagyított képén, $k$-n, azaz az $AB$ szakasz Thalész-körén. Ezért ha $i=\mathrm{1,2}$, akkor az $AB{D}_i\text{'}$ háromszög derékszögű, és a $BD{\text{'}}_i$ befogójához tartozó $A{D}_i$ súlyvonala $\alpha$ szöget zár be az átfogójával. 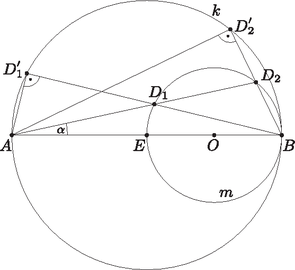  2. ábra     II. megoldás. Használjuk az I. megoldás jelöléseit, legyen továbbá $AB=2$, $BC=2a$, $AC=2b$ és $AF=s$. Az $ABC$ és $AFC$ háromszögek derékszögűek, ezért Pitagorasz tétele szerint $4=4a^2+4b^2$, illetve $s^2=a^2+4b^2$, amikből kapjuk, hogy $\begin{array}{c}{\displaystyle s^2=1+3b^2\mathrm{,}\text{s így}s=\sqrt[]{1+3b^2}\mathrm{,}\text{valamint}{s}^2-a^2=4b^2\mathrm{.}}\end{array}$ (1) Az $\alpha$ szög koszinuszát az $ABF$ háromszög $BF$ oldalára felírt koszinusztételből kifejezve, majd (1)-et felhasználva kapjuk, hogy $\begin{array}{c}{\displaystyle \text{cos}\alpha =\frac{A{B}^2+A{F}^2-B{F}^2}{2\cdot AB\cdot AF}=\frac{4+s^2-a^2}{4s}=\frac{1+b^2}{\sqrt[]{1+3b^2}}\mathrm{.}}\end{array}$ A $2$ átfogójú $ABC$ derékszögű háromszög befogója $2b$, ezért $b$ tetszőleges $0$ és $1$ közti értéket felvehet, így feladatunkat visszavezettük a $\left(0;1\right)$ intervallumon értelmezett $\begin{array}{c}{\displaystyle f\left(b\right)=\frac{1+b^2}{\sqrt[]{1+3b^2}}}\end{array}$ függvény értékkészletének meghatározására. Az $f$ függvényt ugyanezzel a képlettel definiálhatjuk az összes valós számon. Az így kiterjesztett függvény nyilván folytonos az egész számegyenesen, és ezért $\begin{array}{c}{\displaystyle \underset{b\to 0}{\overset{}{\text{lim}}}f\left(b\right)=f\left(0\right)=\mathrm{1,}\text{valamint}\underset{b\to 1}{\overset{}{\text{lim}}}f\left(b\right)=f\left(1\right)=1}\end{array}$ teljesül. A függvénynek a $\left(0;1\right)$ intervallumon lévő minimumát kisebb átalakítás után a számtani és mértani közepek közti egyenlőtlenséget felhasználva határozzuk meg. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{1+b^2}{\sqrt[]{1+3b^2}}}& {\displaystyle =\frac{\frac{1}{3}\left(1+3b^2\right)+\frac{2}{3}}{\sqrt[]{1+3b^2}}=\frac{\sqrt[]{1+3b^2}}{3}+\frac{2}{3\sqrt[]{1+3b^2}}\ge }\hfill \\ \hfill {\displaystyle }& {\displaystyle \ge 2\sqrt[]{\frac{\sqrt[]{1+3b^2}}{3}\cdot \frac{2}{3\sqrt[]{1+3b^2}}}=\frac{2\sqrt[]{2}}{3}\mathrm{.}}\hfill \end{array}}$ A függvény a $\left(0;1\right)$ intervallumon csak $1$-nél kisebb értékeket vesz fel, mert ha $0<b<1$, akkor $b^4<b^2$ miatt ${\left(1+b^2\right)}^2=1+2b^2+b^4<1+3b^2$, tehát $1+b^2<\sqrt[]{1+3b^2}$, és ezért $f\left(b\right)<1$. Így a $\left(0;1\right)$ intervallumon értelmezett $f$ függvény értékkészlete a $\left[\frac{2\sqrt[]{2}}{3}\mathrm{,1}\right)$ intervallum. Ezért $\alpha$ minden olyan hegyesszöget felvesz, amelyre $\frac{2\sqrt[]{2}}{3}\le \text{cos}\alpha <1$ teljesül. Tehát egy derékszögű háromszög átfogója és az egyik befogóhoz tartozó súlyvonala által bezárt szög tetszőleges $0^{\circ }$-nál nagyobb, de $\text{arccos}\frac{2\sqrt[]{2}}{3}\approx 19\mathrm{,}47{}^{\circ }$-nál nem nagyobb értéket felvehet.