Feladat:	B.4615	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kocsis Júlia
Füzet:	2015/március, 144. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, A háromszögek nevezetes pontjai
Hivatkozás(ok):	Feladatok: 2014/március: B.4615

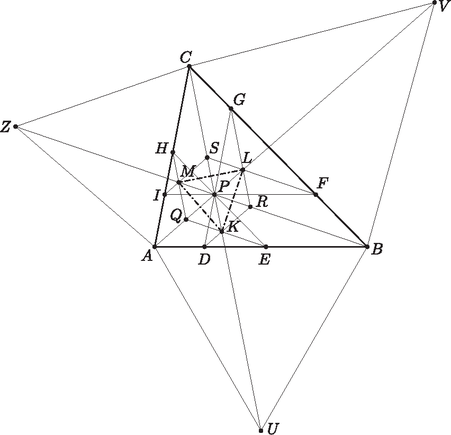
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Ismert, hogy az izogonális pont úgy is megszerkeszthető, hogy a háromszög oldalaira kifelé szabályos háromszögeket szerkesztünk, majd ezek külső csúcsait az eredeti háromszög ellentétes csúcsával összekötjük. A három összekötő szakasz egy pontban, a háromszög izogonális pontjában metszi egymást. Legyenek az $AB$, $BC$ és $CA$ oldalakra kifelé rajzolt szabályos háromszögek harmadik csúcsai rendre $U$, $V$, $Z$. Az is ismert, hogy a $P$-nél keletkező hat darab szög mindegyike ${60}^{\circ }$-os.     A $CU$ egyenes egybeesik a $PK$ egyenessel, hiszen a $PDE$ háromszög minden oldala párhuzamos az $ABC$ háromszög megfelelő oldalaival, tehát a csúcsokból az izogonális pontba menő egyenesek is párhuzamosak. Mivel ezek a két háromszög esetében átmennek a $P$ ponton is, ezért egybeesnek. Ugyanezt beláthatjuk a $GPF$ és $HPI$ háromszögeknél is a megfelelő oldalakkal. Ugyanezzel a módszerrel azt is bizonyíthatjuk, hogy a $HAE$, $DBG$ és $FCI$ háromszögek izogonális pontjai is rajta vannak a $P$ pontot a megfelelő csúccsal összekötő szakaszokon. Legyenek ezek az izogonális pontok rendre $Q$, $R$ és $S$. A $KLM$ háromszög izogonális pontja $P$, mert az eddigiek alapján $MPK\sphericalangle =KPL\sphericalangle =LPM\sphericalangle ={120}^{\circ }$. Most használjuk fel azt a fentebb már említett tulajdonságot, hogy az izogonális pontnál keletkező szögek mindegyike ${60}^{\circ }$. A $K$, $L$, $M$, $Q$, $R$, $S$ pontok mindegyike izogonális pont, tehát a $PKR$, $RPL$, $LPS$, $SPM$, $MPQ$ és $QPK$ háromszögek mindegyike szabályos, egymással egybevágó háromszög. A $KPL$, $LPM$ és $LPM$ háromszögek ${120}^{\circ }$-os szárszögű egyenlő szárú háromszögek, az alapon fekvő szögek ${30}^{\circ }$-osak, a $KLM$ háromszög tehát szabályos.